Question

由点P引三条不共面的射线PA、PB、PC,且cos∠APC=cos∠APB·cos∠BPC,求证:平面APB⊥平面BPC.

Answer 1

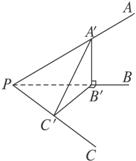
证法一:如图所示,在PA上取一点A′,过A′作A′B′⊥PB于B′,过B′作B′C′⊥PB交PC于C′.

则∠A′B′C′为二面角A-PB-C的平面角.

由余弦定理及三角函数定义并结合已知得.

化简得2PB′²=PA′²+PC′²-A′C′².

又PA′²=PB′²+A′B′²,PC′²=PB′²+BC′²,∴A′C′²=A′B′²+B′C′².

∴∠A′B′C′=90°.

故平面APB⊥平面BPC.

证法二:在PA上取一点A′,过A′作A′B′⊥PB于B′,过B′作B′C′⊥PC于C′点.

在Rt△PA′B′中,cos∠APB=,

在Rt△PB′C′中,cos∠BPC=,

在△PA′C′中,由余弦定理得cos∠APC=.

由已知条件cos∠APB·cos∠BPC=cos∠APC,得

.

化简得2PC′²=PA′²+PC′²-A′C′²,

即A′C′²+PC′²=PA′².

∴∠A′C′P=90°.又PC′⊥B′C′,

∴PC′⊥平面A′B′C′.

∴PC′⊥A′B′.又A′B′⊥PB,∴A′B′⊥平面BPC.又A′B′平面BPA,∴平面APB⊥平面BPC.