题目内容
如果（3a-
）n的展开式中各项系数之和为128，则展开式中a2的系数是（ ）
| 1 | |||
|
| A．-2835 | B．2835 | C．21 | D．-21 |
令a=1，则展开式的各项系数和为128，
即（3-1）n=2n=128，
解得n=7．
∴展开式的通项公式为Tk+1=
(3a)7-k•(-
)k=
a7-
，
令7-
=2，解得k=3，
∴展开式中a2的项为T4=-34
a2=-2835a2，
∴展开式中a2的系数是-2835．
故选：A．
即（3-1）n=2n=128，
解得n=7．
∴展开式的通项公式为Tk+1=
| C | k7 |
| 1 | |||
|
| (-1)k•37-k•C | k7 |
| 5k |
| 3 |
令7-
| 5k |
| 3 |
∴展开式中a2的项为T4=-34
| C | 37 |
∴展开式中a2的系数是-2835．
故选：A．
练习册系列答案
阅读快车系列答案
相关题目
等于 （ ）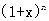 
的展开式中，若第
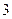项与第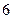
项系数相等，且
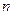等于多少？