题目内容
已知双曲线 的一个焦点在圆x2+y2-4x-5=0上,则双曲线的渐近线方程为 .
的一个焦点在圆x2+y2-4x-5=0上,则双曲线的渐近线方程为 .
【答案】分析:先确定双曲线的焦点坐标,利用焦点在圆x2+y2-4x-5=0上,求得m的值,从而可求双曲线的渐近线方程
解答:解:由题意,双曲线的焦点坐标为
代入圆x2+y2-4x-5=0得
∴m2-8m-128=0
∴m=16
∴双曲线的渐近线方程为
故答案为
点评:本题以双曲线的标准方程为载体,考查双曲线的几何性质,关键是求出双曲线的标准方程.
解答:解:由题意,双曲线的焦点坐标为

代入圆x2+y2-4x-5=0得

∴m2-8m-128=0
∴m=16
∴双曲线的渐近线方程为

故答案为

点评:本题以双曲线的标准方程为载体,考查双曲线的几何性质,关键是求出双曲线的标准方程.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
已知双曲线的一个焦点与抛物线x2=20y的焦点重合,且其渐近线的方程为3x±4y=0,则该双曲线的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为
,则该双曲线的方程为
 B.
B.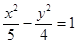 C.
C. D.
D.