题目内容
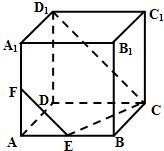
如图所示，在正方体ABCD－A1B1C1D1中，棱长为a，M，N分别为A1B和AC上的点，A1M＝AN＝
，则MN与平面BB1C1C的位置关系是( )
(A)相交 (B)平行 (C)垂直 (D)不能确定
B.分别以C1B1，
C1D1，C1C所在直线为x，y，z轴，建立空间直角坐标系.
∵A1M＝AN＝
a，
∴M(a，
a，
)，N(a，a，a).
∴
＝(－，0，a).
又C1(0,0,0)，D1(0，a,0)，
∴
＝(0，a,0).
∴·＝0.∴⊥.
∵是平面BB1C1C的一个法向量，
且MN
平面BB1C1C，
∴MN∥平面BB1C1C.
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
如图所示，在正方体ABCD-A1B1C1D1中，E为AB的中点
（2011•宝山区二模）如图所示，在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等，则动点P所在曲线形状为（ ）
如图所示，在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等，则动点P所在曲线的形状为（ ）
如图所示，在正方体ABCD-A1B1C1D1中，点E是棱CC1上的一个动点，平面BED1交棱AA1于点F．则下列命题中假命题是（ ）