题目内容
 (2010•潍坊三模)在四棱锥S-ABCD中,ABCD为直角梯形,AB∥CD,∠DAB=90°,SD⊥平面ABCD,E为SC的中点,且AB=AD=l,SD=CD=2.
(2010•潍坊三模)在四棱锥S-ABCD中,ABCD为直角梯形,AB∥CD,∠DAB=90°,SD⊥平面ABCD,E为SC的中点,且AB=AD=l,SD=CD=2.(1)若P为SD上的任意一点,能否在SB上找一点H,使得EH⊥BP?请说明理由;
(2)求直线SB与平面BDE所成角的正弦值.
分析:(1)当H为SB的中点时,EH⊥BP,根据中位线定理可知HE∥BC,根据线面垂直的性质可知SD⊥BC,取CD的中点M,连BM,根据勾股定理的逆定义可知BC⊥BD又BD∩SD=D,满足线面垂直的判定定理所需条件,则BC⊥面SBD,从而EH⊥面SBD,可证得结论;
(2)以DA、DC、DS分别为x、y、z轴建立坐标系,求出向量
、
、
,然后求出平面BDE的法向量为
=(x,y,z)根据cos<
,
>=
可得直线SB与平面BDE所成角的正弦值.
(2)以DA、DC、DS分别为x、y、z轴建立坐标系,求出向量
| BS |
| BD |
| BE |
| n |
| n |
| BS |
| ||||
|
解答:解:(1)当H为SB的中点时,EH⊥BP
∵H、E分别为SB、SC的中点∴HE∥BC
又SD⊥平面ABCD∴SD⊥BC,
由条件知,BD2=AB2+AD2=2
取CD的中点M,连BM,则四边形ABMD为矩形
∴BC2=CM2+BM2=2∴BC2+BD2=CD2
∴BC⊥BD又BD∩SD=D
∴BC⊥面SBD
∴EH⊥面SBD
∴在SB上存在一点H,使得EH⊥BP
(2)∵SD⊥平面ABCD∴SD⊥CD,SD⊥AD
又AB∥CD,∠DAB=90°∴AD⊥CD
以DA、DC、DS分别为x、y、z轴建立坐标系,则
D(0,0,0),B(1,1,0),C(0,2,0),S(0,0,2),E(0,1,1)
∴
=(-1,-1,2),
=(-1,-1,0),
=(-1,0,1)
设平面BDE的法向量为
=(x,y,z)则
即
取x=1,则y=-1,z=1则
=(1,-1,1)
则cos<
,
>=
=
=
∴直线SB与平面BDE所成角的正弦值

∵H、E分别为SB、SC的中点∴HE∥BC
又SD⊥平面ABCD∴SD⊥BC,
由条件知,BD2=AB2+AD2=2
取CD的中点M,连BM,则四边形ABMD为矩形
∴BC2=CM2+BM2=2∴BC2+BD2=CD2
∴BC⊥BD又BD∩SD=D
∴BC⊥面SBD
∴EH⊥面SBD
∴在SB上存在一点H,使得EH⊥BP
(2)∵SD⊥平面ABCD∴SD⊥CD,SD⊥AD
又AB∥CD,∠DAB=90°∴AD⊥CD
以DA、DC、DS分别为x、y、z轴建立坐标系,则
D(0,0,0),B(1,1,0),C(0,2,0),S(0,0,2),E(0,1,1)
∴
| BS |
| BD |
| BE |
设平面BDE的法向量为
| n |
|
|
取x=1,则y=-1,z=1则
| n |
则cos<
| n |
| BS |
| ||||
|
| 2 | ||||
|
| ||
| 3 |
∴直线SB与平面BDE所成角的正弦值
| ||
| 3 |
点评:本题主要考查了线面垂直的判定,以及利用空间向量的方法求线面所成角,同时考查了空间想象能力和推理论证的能力,属于中档题.

练习册系列答案
相关题目
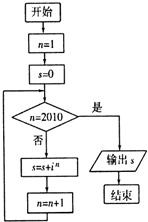 (2010•潍坊三模)运行如图所示的程序框图输出的结果是(其中i是虚数单位)( )
(2010•潍坊三模)运行如图所示的程序框图输出的结果是(其中i是虚数单位)( )