题目内容

若规定
.
 a，b 
 c，d 
.
=ad-bc，则不等式log2
.
 1，1 
 1，x 
.
＜-1的解集是
(1，
3
2
)
(1，
3
2
)
．
分析：根据二阶行列式的定义原不等式可化为：log2（x-1）＜-1，再利用对数函数的单调性去掉对数符号得出关于x的整式不等式，即可求解．
解答：解：原不等式可化为：
log2（x-1）＜-1，
即：log2(x-1)＜log2
1
2

⇒0＜x-1＜
1
2
，⇒1＜x＜
3
2
，
故答案为：(1，
3
2
)．
点评：本小题主要考查函数单调性的应用、二阶行列式的定义、不等式的解法等基础知识，考查运算求解能力，考查化归与转化思想．属于基础题．
练习册系列答案
相关题目
16、设I={1，2，3，4}，A与B是I的子集，若A∩B={2，3}，则称（A，B）为一个“理想配集”，那么符合此条件的“理想配集”的个数是
9
．（规定（A，B）与（B，A）是两个不同的“理想配集”）
设I={1，2，3，4}，A与B是I的子集，若A∩B={1，3}，则称（A，B）为一个“理想配集”．那么符合此条件的“理想配集”的个数是（规定（A，B）与（B，A）是两个不同的“理想配集”）（　　）
设I={1，2，3，4}，A与B是I的子集，若A∩B={1，3}，则称（A，B）是一个“理想配集”规定（A，B）与（B，A）是两不同的配集，那么符合条件的“理想配集”个数为（　　）
规定min{a，b}表示a，b两个数中的最小的数，min{a，b}=
a，a≤b
b，a＞b
，若函数f（x）=min{|x|，|x+t|}的图象关于直线x=-
1
2
对称，则t的值是（　　）
规定min{a，b}表示a，b两个数中的最小的数，min{a，b}=，若函数f（x）=min{|x|，|x+t|}的图象关于直线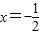对称，则t的值是（ ）
A．-1
B．1
C．-2
D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网