题目内容
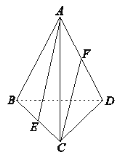
【题目】如图,在三棱锥![]() 中,底面是边长为
中,底面是边长为![]() 的正三角形,
的正三角形,![]() ,且
,且![]() ,
,![]() 分别是
分别是![]() ,
,![]() 中点,则异面直线
中点,则异面直线![]() 与
与![]() 所成角的余弦值为__________.
所成角的余弦值为__________.
【答案】![]()
【解析】
连结DE,到DE中点P,连结PF、PC,则PF∥AE,从而∠PFC是异面直线AE和CF所成角的余弦值,由此能求出异面直线AE和CF所成角的余弦值.
解:因为三棱锥ABCD中,底面是边长为2的正三角形,AB=AC=AD=4,
所以三棱锥ABCD为正三棱锥;
连结DE,取DE中点P,连结PF、PC,

∵正三棱锥ABCD的侧棱长都等于4,底面正三角形的边长2,
点E、F分别是棱BC、AD的中点,
∴PF∥AE,
∴∠PFC是异面直线AE和CF所成角的余弦值,![]() ,
,![]() ,
,![]() ,
,  ,
, .
.
∴异面直线AE和CF所成角的余弦值为![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目