题目内容
已知f（x）=2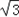
sinx+
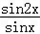
（1）求f（x）的最大值，及当取最大值时x的取值集合．
（2）在三角形ABC中，a，b，c分别是角A，B，C所对的边，对定义域内任意x，有f（x）≤
f（A），若a=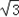
，求
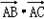的最大值．
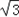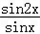
sinx+（1）求f（x）的最大值，及当取最大值时x的取值集合．
（2）在三角形ABC中，a，b，c分别是角A，B，C所对的边，对定义域内任意x，有f（x）≤
f（A），若a=
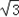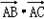，求的最大值．解：（1）f（x）=2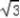
sinx+ 
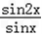=2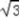
sinx+2cosx=4sin（x+ 
）
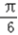∴当x+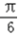
=2kπ+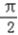 
（k∈Z）时，f（x）取得最大值为4
∴f（x）的最大值为4，取最大值时x的取值集合为{x|x=2kπ+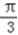
，k∈Z}．
（2）对定义域内任意x，有f（x）≤f（A），
∴f（A）为f（x）为最大值
∴f（A）=4即sin（A+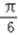
）=1
∴0＜A＜π，
∴A=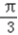
∴ 
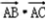=cbcosA=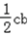 
又∵a2=b2+c2﹣2bccosA，a=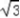
∴3=b2+c2﹣bc≥bc（当b=c时取等号）
∴bc≤3
∴
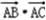的最大值
，此时b=c=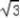 
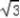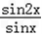sinx+ =2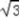 sinx+2cosx=4sin（x+ 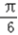） ∴当x+
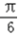=2kπ+ 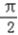（k∈Z）时，f（x）取得最大值为4 ∴f（x）的最大值为4，取最大值时x的取值集合为{x|x=2kπ+
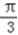，k∈Z}．（2）对定义域内任意x，有f（x）≤f（A），
∴f（A）为f（x）为最大值
∴f（A）=4即sin（A+
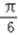）=1 ∴0＜A＜π，
∴A=
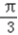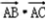∴ =cbcosA=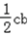 又∵a2=b2+c2﹣2bccosA，a=
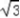
∴3=b2+c2﹣bc≥bc（当b=c时取等号）
∴bc≤3
∴
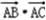的最大值 ，此时b=c=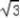 
练习册系列答案
相关题目
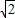倍，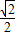
倍，
倍，
个单位，⑧向右平移
个单位，
个单位，⑩向右平移
个单位，