题目内容
已知n为正整数,曲线![]() 总经过定点(
总经过定点(![]() ,0)
,0)
(1)求证点列:![]() 在同一直线上
在同一直线上
(2)若记 f(k)+f(k+1)+f(k+2)+![]() f(n)=
f(n)=![]() ,其中k, n为正整数且k
,其中k, n为正整数且k![]() n
n
求证:![]() (n
(n![]() )
)
解:(1)设切线L![]() 的斜率为k
的斜率为k![]() ,由切线过点
,由切线过点![]() 得切线方程为y=k
得切线方程为y=k![]() (x+1)
(x+1)
则方程组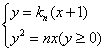 有解
有解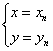 , ……1分
, ……1分
由方程组用代入法消去y化简得 ![]() (*)
(*)
有![]() ………2分
………2分
代入方程(*),得![]()
![]()
即![]() 在同一直线x=1上 …………………4分
在同一直线x=1上 …………………4分
(2) 解:由(1)可知 ![]() ………5分
………5分
设函数 F(x)=![]()

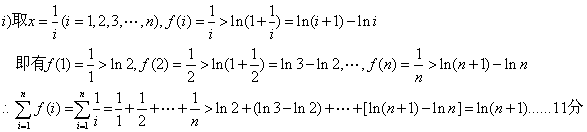
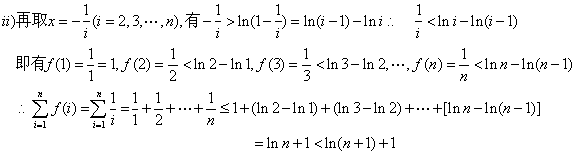 综合上述有
综合上述有![]() …………………14分
…………………14分


练习册系列答案
相关题目

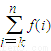 ,其中k,n为正整数且k≤n)
,其中k,n为正整数且k≤n)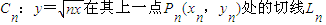 总经过定点(-a,0)(n∈N*)
总经过定点(-a,0)(n∈N*)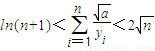 (n∈N*)
(n∈N*)