题目内容
三棱锥P-ABC中，PA=PB=PC=2，AB⊥BC，AB=1，BC=
，则点P到平面ABC的距离为 ．
| 3 |
分析：要求点P到平面ABC的距离，先得找出距离所在，即点P在平面ABC上的射影O的位置，由题意可得它是直角三角形的外心．从而求出PO的长即可．
解答：
解：∵PA=PB=PC=2
∴点P在平面ABC上的射影O是直角三角形ABC斜边上的中心，
故PO即为所求的距离，
在直角三角形PBO中，
PB=2，OB=1，
∴PO=
，
故填：
解：∵PA=PB=PC=2∴点P在平面ABC上的射影O是直角三角形ABC斜边上的中心，
故PO即为所求的距离，
在直角三角形PBO中，
PB=2，OB=1，
∴PO=
| 3 |
故填：
| 3 |
点评：本题主要考查了点、线、面间的距离计算，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
相关题目
如图，在三棱锥P-ABC中，△PAB是等边三角形，∠PAC=∠PBC=90°．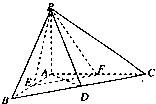
如图，在三棱锥P-ABC中，
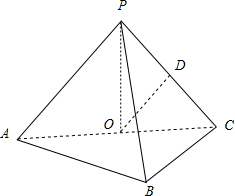如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．
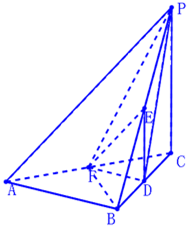如图，在三棱锥P-ABC中，PC⊥平面ABC，△ABC为正三角形，D、E、F分别是BC，PB，CA的中点．