题目内容
平面内已知两点A（0，2）、B（0，-2），若动点P满足|PA|+|PB|=4，则点P的轨迹是
- A.椭圆
- B.双曲线
- C.抛物线
- D.线段
D
分析：根据|PA|+|PB|=4，且线段AB的长等于4，可得点P位于线段AB上运动，由此可得本题的答案．
解答：∵点A（0，2）、B（0，-2），∴|AB|=4
又∵动点P满足|PA|+|PB|=4，
∴点P在直线AB上，且在A、B之间（含站点）
由此可得，点P的轨迹是线段AB
故选：D
点评：本题给出动点P与定点A、B，求点P的轨迹，着重考查了椭圆的定义和轨迹方程的求法等知识，属于基础题．
分析：根据|PA|+|PB|=4，且线段AB的长等于4，可得点P位于线段AB上运动，由此可得本题的答案．
解答：∵点A（0，2）、B（0，-2），∴|AB|=4
又∵动点P满足|PA|+|PB|=4，
∴点P在直线AB上，且在A、B之间（含站点）
由此可得，点P的轨迹是线段AB
故选：D
点评：本题给出动点P与定点A、B，求点P的轨迹，着重考查了椭圆的定义和轨迹方程的求法等知识，属于基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
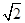倍后得到点Q(x,
·
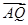=1. 
的直线L交曲线C于M、N两点，且
+
+
=
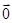，试求△MNH的面积.
倍后得到点Q(x,
·
=1.
的直线l交曲线C于M、N两点，且
+
+
=
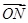，试求△MNH的面积.