题目内容
设函数y=f(x)是定义在R上的函数,并且满足下面三个条件;
①对任意正数x,y,都有f(xy)=f(x)+f(y);
②当x>1时,f(x)<0;
③f(3)=-1.
(Ⅰ)求 的值;
的值;
(Ⅱ)证明f(x)在R+是减函数;
(Ⅲ)如果不等式f(x)+f(2-x)<2成立,求x的取值范围.
解:(Ⅰ)令x=y=1易得f(1)=0,
而f(9)=f(3)+f(3)=-1-1=-2,
且
(Ⅱ)取定义域中的任意的x1,x2
且
∴
∴f(x)在R+上为减函数.
(Ⅲ)由条件(1)及(Ⅰ)的结果得: ,
,
由可(Ⅱ)得: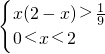
解得x的范围是 .
.
分析:(Ⅰ)求 的值;令x=y=1代入f(xy)=f(x)+f(y)即可求得f(1).同理求出f(9)后,令x=9,xy=1,代入等式即可求得答案;
的值;令x=y=1代入f(xy)=f(x)+f(y)即可求得f(1).同理求出f(9)后,令x=9,xy=1,代入等式即可求得答案;
(Ⅱ)证明f(x)在R+是减函数;取定义域中的任意的x1,x2,且0<x1<x2然后根据关系式f(xy)=f(x)+f(y),证明f(x1)>f(x2)即可;
(Ⅲ)如果不等式f(x)+f(2-x)<2成立,求x的取值范围,由(Ⅰ)的结果得: ,再根据单调性,列出不等式.解出取值范围即可.
,再根据单调性,列出不等式.解出取值范围即可.
点评:此题主要考查抽象函数的一系列问题.其中涉及到函数单调性的证明,函数值的求解问题.属于综合性问题,涵盖知识点较多,属于中档题目.
而f(9)=f(3)+f(3)=-1-1=-2,
且

(Ⅱ)取定义域中的任意的x1,x2
且

∴

∴f(x)在R+上为减函数.
(Ⅲ)由条件(1)及(Ⅰ)的结果得:
 ,
,由可(Ⅱ)得:
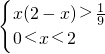
解得x的范围是
 .
.分析:(Ⅰ)求
 的值;令x=y=1代入f(xy)=f(x)+f(y)即可求得f(1).同理求出f(9)后,令x=9,xy=1,代入等式即可求得答案;
的值;令x=y=1代入f(xy)=f(x)+f(y)即可求得f(1).同理求出f(9)后,令x=9,xy=1,代入等式即可求得答案;(Ⅱ)证明f(x)在R+是减函数;取定义域中的任意的x1,x2,且0<x1<x2然后根据关系式f(xy)=f(x)+f(y),证明f(x1)>f(x2)即可;
(Ⅲ)如果不等式f(x)+f(2-x)<2成立,求x的取值范围,由(Ⅰ)的结果得:
 ,再根据单调性,列出不等式.解出取值范围即可.
,再根据单调性,列出不等式.解出取值范围即可.点评:此题主要考查抽象函数的一系列问题.其中涉及到函数单调性的证明,函数值的求解问题.属于综合性问题,涵盖知识点较多,属于中档题目.

练习册系列答案
相关题目