题目内容
 已知函数f(x)=
已知函数f(x)=
|
(1)求f(-1)以及m的值;
(2)在给出的直角坐标系中画出y=f(x)的图象;
(3)若函数g(x)=f(x)-2k+1有三个零点,求实数k的取值范围.
分析:(1)由函数f(x)是奇函数及f(-1)与f(1)的关系可求f(-1),根据f(x)解析式表示出f(-1)得一关于m的方程可求m值;
(2)由(1)可知f(x)的解析式,根据解析式即可画出其图象;
(3)数形结合,转化为两函数y=f(x)与y=2k-1图象的交点个数问题即可解决.
(2)由(1)可知f(x)的解析式,根据解析式即可画出其图象;
(3)数形结合,转化为两函数y=f(x)与y=2k-1图象的交点个数问题即可解决.
解答: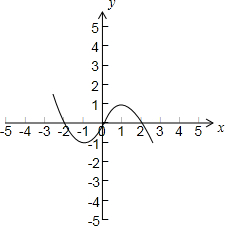 (1)∵f(x)为奇函数,且f(1)=-12+2×1=1,∴f(-1)=-f(1)=-1.
(1)∵f(x)为奇函数,且f(1)=-12+2×1=1,∴f(-1)=-f(1)=-1.
而f(-1)=(-1)2+m(-1)=1-m=-1,所以m=2.
故f(-1)=-1,m=2.
(2)由(1)知函数f(x)=
,则y=f(x)的图象如右图所示:
(3)若函数g(x)=f(x)-2k+1有三个零点,即函数y=f(x)与函数y=2k-1的图象有三个交点,
由图象知:-1<2k-1<1,解得0<k<1.
故实数k的取值范围为(0,1).
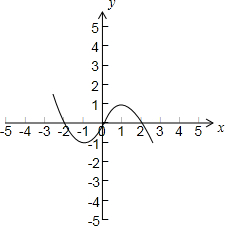 (1)∵f(x)为奇函数,且f(1)=-12+2×1=1,∴f(-1)=-f(1)=-1.
(1)∵f(x)为奇函数,且f(1)=-12+2×1=1,∴f(-1)=-f(1)=-1.而f(-1)=(-1)2+m(-1)=1-m=-1,所以m=2.
故f(-1)=-1,m=2.
(2)由(1)知函数f(x)=
|
(3)若函数g(x)=f(x)-2k+1有三个零点,即函数y=f(x)与函数y=2k-1的图象有三个交点,
由图象知:-1<2k-1<1,解得0<k<1.
故实数k的取值范围为(0,1).
点评:本题考查了函数的奇偶性、函数作图及函数零点问题,有一定综合性.本题三问环环相扣,由浅入深,解决本题关键是掌握有关基本概念、基本方法及转化、数形结合思想.

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|