题目内容
7.如图,圆O的内接△ABC中,M是BC的中点,AC=3,AB=$\sqrt{7}$,则$\overrightarrow{AO}•\overrightarrow{AM}$=4.
分析 如图所示,分别取AB,AC的中点D,E,连接OD,OE,利用“垂经定理”的推论可得OD⊥AB,OE⊥AC.于是$\overrightarrow{AB}•\overrightarrow{AO}$=$\frac{1}{2}{\overrightarrow{AB}}^{2}$,$\overrightarrow{AC}•\overrightarrow{AO}$=$\frac{1}{2}{\overrightarrow{AC}}^{2}$.由M是BC的中点,
可得$\overrightarrow{AM}$=$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$.即可得出.
解答 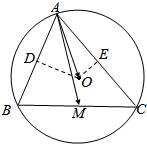 解:如图所示,分别取AB,AC的中点D,E,连接OD,OE,
解:如图所示,分别取AB,AC的中点D,E,连接OD,OE,
则OD⊥AB,OE⊥AC.
∴$\overrightarrow{AB}•\overrightarrow{AO}$=$\frac{1}{2}{\overrightarrow{AB}}^{2}$=$\frac{1}{2}×(\sqrt{7})^{2}$=$\frac{7}{2}$,$\overrightarrow{AC}•\overrightarrow{AO}$=$\frac{1}{2}{\overrightarrow{AC}}^{2}$=$\frac{1}{2}×{3}^{2}$=$\frac{9}{2}$.
∵M是BC的中点,
∴$\overrightarrow{AM}$=$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$.
∴$\overrightarrow{AO}•\overrightarrow{AM}$=$\overrightarrow{AO}•\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$=$\frac{1}{2}\overrightarrow{AB}•\overrightarrow{AO}$$+\frac{1}{2}\overrightarrow{AC}•\overrightarrow{AO}$=$\frac{1}{2}×(\frac{7}{2}+\frac{9}{2})$=4.
故答案为:4.
点评 本题考查了“垂经定理”的推论、向量的数量积运算性质、向量的平行四边形法则,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |