题目内容
设向量 满足
满足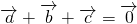 ,
, ,则
,则 =
=
- A.1
- B.2
- C.4
- D.5
D
分析:要求向量的模,求模时一般先求模的平方,而本题直接求模的平方,故题目省掉一步开方,也使同学们避免了一个错误,根据三个向量和为零,得到要求向量的表示式,再就是向量垂直时数量积为零.
解答:∵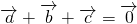
∴
∵ ⊥
⊥ ,
,
∴
∴ =
=
=
=5
点评:两个向量的数量积称为内积,写成a×b;今后要学到两个向量的外积a×b,而a×b是两个向量的数量的积,书写时要严格区分.符号“•”在向量运算中不是乘号,既不能省略,也不能用“×”代替.
分析:要求向量的模,求模时一般先求模的平方,而本题直接求模的平方,故题目省掉一步开方,也使同学们避免了一个错误,根据三个向量和为零,得到要求向量的表示式,再就是向量垂直时数量积为零.
解答:∵
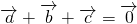
∴

∵
 ⊥
⊥ ,
,∴

∴
 =
=
=

=5
点评:两个向量的数量积称为内积,写成a×b;今后要学到两个向量的外积a×b,而a×b是两个向量的数量的积,书写时要严格区分.符号“•”在向量运算中不是乘号,既不能省略,也不能用“×”代替.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 满足:
满足: ,则
,则 等于( )
等于( )

 满足
满足 ,
, ,则
,则 =( )
=( ) 满足
满足 ,
, ,则
,则 =
= 满足
满足 ,
, ,则
,则



