题目内容
已知函数f(x)=cosxsinx(x∈R),给出下列四个命题:①若f(x1)=-f(x2),则x1=-x2 ②f(x)的最小正周期是2π;
③f(x)在区间[-
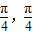 ]上是增函数; ④f(x)的图象关于直线x=
]上是增函数; ④f(x)的图象关于直线x=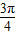 对称;
对称;⑤当x∈[-
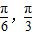 时,f(x)的值域为[-
时,f(x)的值域为[-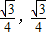 ].
].其中正确的命题为( )
A.①②④
B.③④⑤
C.②③
D.③④
【答案】分析:根据题意把函数化简为f(x)= sin2x,①可以举例判断其实错误的.②根据周期公式可得函数周期为π.③求出函数的所以单调增区间即可得到③正确.④求出函数的所有对称轴可验证得④正确.⑤根据题意求出2x∈[
sin2x,①可以举例判断其实错误的.②根据周期公式可得函数周期为π.③求出函数的所以单调增区间即可得到③正确.④求出函数的所有对称轴可验证得④正确.⑤根据题意求出2x∈[ ],所以sin2x∈[
],所以sin2x∈[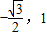 ],进而求出函数的值域,即可得到⑤错误.
],进而求出函数的值域,即可得到⑤错误.
解答:解:由题意可得:f(x)=cosxsinx= sin2x,
sin2x,
①f(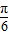 )=-f(
)=-f(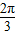 ),但是不满足x1=-x2,所以①错误.
),但是不满足x1=-x2,所以①错误.
②根据周期公式可得:f(x)= sin2x的周期为π.所以②错误.
sin2x的周期为π.所以②错误.
③f(x)= sin2x的单调增区间为[kπ-
sin2x的单调增区间为[kπ-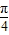 ,kπ+
,kπ+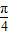 ],(k∈Z),显然③正确.
],(k∈Z),显然③正确.
④f(x)= sin2x的所有对称轴为x=
sin2x的所有对称轴为x=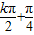 ,显然④正确.
,显然④正确.
⑤f(x)= sin2x,因为x∈∈[-
sin2x,因为x∈∈[-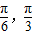 ]时,所以2x∈[
]时,所以2x∈[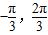 ],所以sin2x∈[
],所以sin2x∈[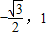 ],所以f(x)的值域为[
],所以f(x)的值域为[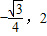 ].所以⑤错误.
].所以⑤错误.
故选D.
点评:解决此类问题的关键是熟练掌握二倍角公式,以及三角函数的有关性质(单调性,周期性,奇偶性,对称性等).
 sin2x,①可以举例判断其实错误的.②根据周期公式可得函数周期为π.③求出函数的所以单调增区间即可得到③正确.④求出函数的所有对称轴可验证得④正确.⑤根据题意求出2x∈[
sin2x,①可以举例判断其实错误的.②根据周期公式可得函数周期为π.③求出函数的所以单调增区间即可得到③正确.④求出函数的所有对称轴可验证得④正确.⑤根据题意求出2x∈[ ],所以sin2x∈[
],所以sin2x∈[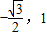 ],进而求出函数的值域,即可得到⑤错误.
],进而求出函数的值域,即可得到⑤错误.解答:解:由题意可得:f(x)=cosxsinx=
 sin2x,
sin2x,①f(
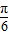 )=-f(
)=-f(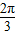 ),但是不满足x1=-x2,所以①错误.
),但是不满足x1=-x2,所以①错误.②根据周期公式可得:f(x)=
 sin2x的周期为π.所以②错误.
sin2x的周期为π.所以②错误.③f(x)=
 sin2x的单调增区间为[kπ-
sin2x的单调增区间为[kπ-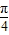 ,kπ+
,kπ+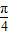 ],(k∈Z),显然③正确.
],(k∈Z),显然③正确.④f(x)=
 sin2x的所有对称轴为x=
sin2x的所有对称轴为x=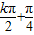 ,显然④正确.
,显然④正确.⑤f(x)=
 sin2x,因为x∈∈[-
sin2x,因为x∈∈[-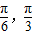 ]时,所以2x∈[
]时,所以2x∈[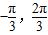 ],所以sin2x∈[
],所以sin2x∈[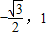 ],所以f(x)的值域为[
],所以f(x)的值域为[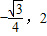 ].所以⑤错误.
].所以⑤错误.故选D.
点评:解决此类问题的关键是熟练掌握二倍角公式,以及三角函数的有关性质(单调性,周期性,奇偶性,对称性等).

练习册系列答案
相关题目
已知函数f(x)=
,则关于x的方程f2(x)+bf(x)+c=0有5个不同实数解的充要条件是( )
|
| A、b<-2且c>0 |
| B、b>-2且c<0 |
| C、b<-2且c=0 |
| D、b≥-2且c=0 |
 已知函数f(x)的图象如图所示,则函数的值域为( )
已知函数f(x)的图象如图所示,则函数的值域为( )