题目内容
 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
分析:根据题意知|AC|=|CF|=-c-(-
) =
,|BF|=
•cot30°=
.
∵|BD|=|DF|=c+
,则
=
,整理得e4-4e2+1=0.由此可求出椭圆的离心率.
| a2 |
| c |
| b2 |
| c |
| ||
| c |
| ||
| c |
∵|BD|=|DF|=c+
| a2 |
| c |
| 2(a2+c2) 2 |
| c2 |
| 6(a2-c2) 2 |
| c2 |
解答:解:由题意知|AC|=|CF|=-c-(-
)=
,
∴|AF|=
,|BF|=
•cot30°=
.
∵|BD|=|DF|=c+
,∴|BF|=
(c+
)=
,
∴
=
,整理得e4-4e2+1=0.
解得e2=2-
或e2=2+
(舍去),
∴e=
或e=
(舍去),
答案:
.
| a2 |
| c |
| b2 |
| c |
∴|AF|=
| ||
| c |
| ||
| c |
| ||
| c |
∵|BD|=|DF|=c+
| a2 |
| c |
| 2 |
| a2 |
| c |
| ||
| c |
∴
| 2(a2+c2)2 |
| c2 |
| 6(a2-c2)2 |
| c2 |
解得e2=2-
| 3 |
| 3 |
∴e=
| ||||
| 2 |
| ||||
| 2 |
答案:
| ||||
| 2 |
点评:结合图象求解,事半功倍.

练习册系列答案
相关题目
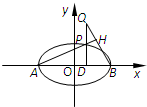 如图,已知椭圆
如图,已知椭圆 (2013•汕头一模)如图.已知椭圆
(2013•汕头一模)如图.已知椭圆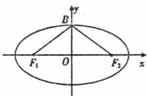 (2012•安徽模拟)如图,已知椭圆
(2012•安徽模拟)如图,已知椭圆 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆 如图,已知椭圆
如图,已知椭圆