题目内容
已知O是△ABC内任意一点，连结AO、BO、CO并延长交对边于A′,B′,C′,则
+
+
=1,这是一道平面几何题,其证明常采用“面积法”.
++=
+
+
=
=1，
请运用类比思想，对于空间中的四面体V—BCD，存在什么类似的结论？并用体积法证明.
在四面体O—BCD与V—BCD中：
=
=
=
.
解析:
在四面体V—BCD中，任取一点O，连结VO、DO、BO、CO并延长分别交四个面于E、F、G、H点.
则+
+
+
=1.
在四面体O—BCD与V—BCD中：===.
同理有：=
；=
；=
，
∴+++
=
=
=1.
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
=
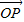[（1-λ）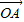
+（1-λ）
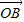+（1+2λ）
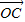]（λ∈R且λ≠0），则点P的轨迹一定通过△ABC的 ．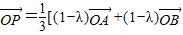
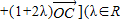且λ≠1，则P的轨迹一定通过△ABC的（ ）