题目内容
已知函数f(x)=logax(a>0且a≠1).
(Ⅰ)若函数f(x)在[2,3]上的最大值与最小值的和为2,求a的值;
(Ⅱ)将函数f(x)图象上所有的点向左平移2个单位长度,再向下平移1个单位长度,所得函数图象不经过第二象限,求a的取值范围.
解:(Ⅰ)因为函数f(x)=logax在[2,3]上是单调函数,所以,loga3+loga2=2.
所以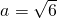 .
.
(Ⅱ)依题意,所得函数g(x)=loga(x+2)-1,由g(x)函数图象恒过(-1,-1)点,且不经过第二象限,
可得 ,即
,即 ,解得a≥2.所以,a的取值范围是[2,+∞).
,解得a≥2.所以,a的取值范围是[2,+∞).
分析:(Ⅰ)因为函数f(x)=logax在[2,3]上是单调函数,所以,loga3+loga2=2,解方程求得a的值.
(Ⅱ)依题意,所得函数g(x)=loga(x+2)-1,由题意可得可 ,由此求出a的取值范围.
,由此求出a的取值范围.
点评:本题考查对数函数的单调性和特殊点,函数图象的平移变换规律,对数函数的图象和性质,得到 ,
,
是解题的难点.
所以
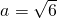 .
.(Ⅱ)依题意,所得函数g(x)=loga(x+2)-1,由g(x)函数图象恒过(-1,-1)点,且不经过第二象限,
可得
 ,即
,即 ,解得a≥2.所以,a的取值范围是[2,+∞).
,解得a≥2.所以,a的取值范围是[2,+∞).分析:(Ⅰ)因为函数f(x)=logax在[2,3]上是单调函数,所以,loga3+loga2=2,解方程求得a的值.
(Ⅱ)依题意,所得函数g(x)=loga(x+2)-1,由题意可得可
 ,由此求出a的取值范围.
,由此求出a的取值范围.点评:本题考查对数函数的单调性和特殊点,函数图象的平移变换规律,对数函数的图象和性质,得到
 ,
,是解题的难点.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目