题目内容
(本题满分12分)
已知函数f (x)=-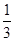 ax3+
ax3+ x2+(a-1)x-
x2+(a-1)x-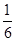 (x>0),(aÎR).
(x>0),(aÎR).
(Ⅰ)当0<a< 时,讨论f (x)的单调性;
时,讨论f (x)的单调性;
(Ⅱ)若f (x)在区间(a, a+1)上不具有单调性,求正实数a的取值范围.
已知函数f (x)=-
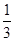 ax3+
ax3+ x2+(a-1)x-
x2+(a-1)x-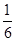 (x>0),(aÎR).
(x>0),(aÎR).(Ⅰ)当0<a<
 时,讨论f (x)的单调性;
时,讨论f (x)的单调性;(Ⅱ)若f (x)在区间(a, a+1)上不具有单调性,求正实数a的取值范围.
(1)当0<a< 时,f (x)在(0,1),(
时,f (x)在(0,1),(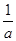 -1,+¥)递减;在(1,
-1,+¥)递减;在(1, 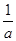 -1)递增
-1)递增
(2)(0, )∪(
)∪( ,1).
,1).
 时,f (x)在(0,1),(
时,f (x)在(0,1),(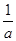 -1,+¥)递减;在(1,
-1,+¥)递减;在(1, 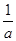 -1)递增
-1)递增(2)(0,
 )∪(
)∪( ,1).
,1).试题分析:解:(Ⅰ) f (x)的定义域为
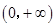 .
.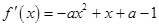 =-a(x-1)[x-(
=-a(x-1)[x-(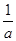 -1)]. ……2分
-1)]. ……2分当0<a<
 时,
时,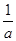 -1>1,
-1>1,∴f (x)在(0,1),(
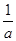 -1,+¥)递减;在(1,
-1,+¥)递减;在(1, 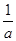 -1)递增; ……4分
-1)递增; ……4分(Ⅱ) f (x)在区间
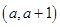 上不具有单调性等价于f (x)在区间
上不具有单调性等价于f (x)在区间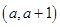 内至少有一个极值点. ……5分
内至少有一个极值点. ……5分①当a=
 时,f ¢(x)=-
时,f ¢(x)=- (x-1)2≤0Þf (x)在
(x-1)2≤0Þf (x)在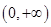 上递减,不合题意; …7分
上递减,不合题意; …7分②当a≥1时,f ¢(x)=0的两根为x1=1,x2=
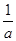 -1,∵
-1,∵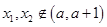 ,故不合题意;③当
,故不合题意;③当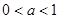 ,且a≠
,且a≠ 时,f (x)在区间
时,f (x)在区间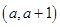 上不具有单调性等价于:
上不具有单调性等价于: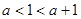 或
或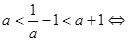
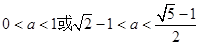
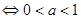
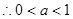 ,且a≠
,且a≠ . ……11分
. ……11分综上可知,所求
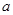 的取值范围是(0,
的取值范围是(0, )∪(
)∪( ,1). ……12分
,1). ……12分点评:这类问题的解决一般主要涉及两类题型,求解单调区间,同时证明不等式恒成立问题。前者经常要对于参数分类讨论,注意对于一元二次不等式的熟练运用,是解决这个题型的关键,后者主要是求解函数的最值来证明不等式。如果递增,则说明函数在给定区间上导数恒大于等于零,反之,则恒小于等于零。来分离参数的思想求解参数的范围。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
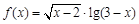 的定义域是
的定义域是  ,如果
,如果 ,则
,则 的取值范围是 .
的取值范围是 .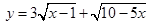 的最大值是( )
的最大值是( )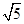
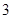
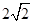
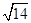
 的定义域是____________.
的定义域是____________. 的值域是( )
的值域是( )



 的定义域为A,若
的定义域为A,若 ,则
,则 的取值范围为 .
的取值范围为 . 的定义域为
的定义域为 ,满足
,满足 ,当
,当 时,
时, ,则
,则 等( )
等( )



 的定义域为( )
的定义域为( )


