题目内容
求经过直线3x-2y+1=0和x+3y+4=0的交点,且垂直于直线x+3y+4=0的直线l的方程.
直线l的方程为3x-y+2=0.
本题主要考查有关直线方程的知识及综合运用知识的能力.可应用直线的点斜式求解;或应用与直线Ax+By+C=0垂直的直线可设为Bx-Ay+C′=0,
从而求解;也可应用过直线A1x+B1y+C1=0和直线A2x+B2y+C2=0的交点的直线可设为
(A1x+B1y+C1)+λ(A2x+B2y+C2)=0,从而求解.
解法一:解方程组
得交点坐标为(-1,-1).
又由题设知k1=3,
∴直线l的方程为y+1=3(x+1),
即3x-y+2=0.
解法二:由题设知k2=3,故可设直线l的方程为3x-y+C=0.
∵l过交点(-1,-1),
∴-3+1+C=0.∴C=2.
故直线l的方程为3x-y+2=0.
解法三:设直线l的方程为
(3x-2y+1)+λ(x+3y+4)=0,
即(3+λ)x+(3λ-2)y+4λ+1=0.
∵l与直线x+3y+4=0垂直,
∴- =3.∴λ=
=3.∴λ= .
.
于是直线l的方程为3x-y+2=0.
从而求解;也可应用过直线A1x+B1y+C1=0和直线A2x+B2y+C2=0的交点的直线可设为
(A1x+B1y+C1)+λ(A2x+B2y+C2)=0,从而求解.
解法一:解方程组

得交点坐标为(-1,-1).
又由题设知k1=3,
∴直线l的方程为y+1=3(x+1),
即3x-y+2=0.
解法二:由题设知k2=3,故可设直线l的方程为3x-y+C=0.
∵l过交点(-1,-1),
∴-3+1+C=0.∴C=2.
故直线l的方程为3x-y+2=0.
解法三:设直线l的方程为
(3x-2y+1)+λ(x+3y+4)=0,
即(3+λ)x+(3λ-2)y+4λ+1=0.
∵l与直线x+3y+4=0垂直,
∴-
 =3.∴λ=
=3.∴λ= .
.于是直线l的方程为3x-y+2=0.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 )
)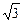 +1),以120°的倾斜角投射到l上,经过l反射,求反射光线所在直线的方程.
+1),以120°的倾斜角投射到l上,经过l反射,求反射光线所在直线的方程. x-y-1=0到直线x-ay=0的角为
x-y-1=0到直线x-ay=0的角为 ,则实数a等于
,则实数a等于
 ,在坐标轴上求一点
,在坐标轴上求一点 ,使直线
,使直线 的倾斜角为
的倾斜角为 .
. ,
, ,
, ,
, 四点共线,求直线方程
四点共线,求直线方程 .
.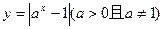 图象有两个交点,则a的取值范围是
图象有两个交点,则a的取值范围是