题目内容
【题目】已知函数
的图象与函数
的图象关于
轴对称，若函数
与函数
在区间
上同时单调递增或同时单调递减，则实数
的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
，即
，当两个函数区间
上同时单调递增时， 
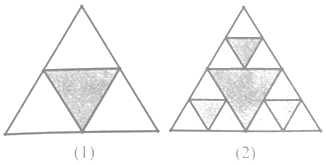
与
的图象如图1所示，易知
，解得
，当两个函数单调递减时
与
的图象如图2所示，此时
关于
轴对称的函数
不可能在
上为减函数，综上所述， 
，故选A.
【思路点睛】本题主要考查数学解题过程中的数形结合思想和化归思想，以及函数的单调性，属于难题.数形结合是根据数量与图形之间的对应关系，通过数与形相互转化来解决数学问题，这种思想方法在解题中运用的目的是化抽象为直观，通过直观的图像解决抽象问题，尤其在解决选择题、填空题时发挥着奇特的功效，大大提高了解题能力与速度.
练习册系列答案
相关题目
【题目】2016年高一新生入学后，为了了解新生学业水平，某区对新生进行了水平测试，随机抽取了50名新生的成绩，其相关数据统计如下：
分数段 | 频数 | 选择题得分24分以上（含24分） |
| 5 | 2 |
| 10 | 4 |
| 15 | 12 |
| 10 | 6 |
| 5 | 4 |
| 5 | 5 |
（Ⅰ）若从分数在
， 
的被调查的新生中各随机选取2人进行追踪调查，求恰好有2名新生选择题得分不足24分的概率；
（Ⅱ）在（Ⅰ）的条件下，记选中的4名新生中选择题得分不足24分的人数为
，求随机变量
的分布列和数学期望.
