题目内容
 函数f(x)=Asinωx的图象如图所示,若
函数f(x)=Asinωx的图象如图所示,若 ,则cosθ-sinθ的值为( )
,则cosθ-sinθ的值为( )A.

B.

C.

D.

【答案】分析:根据最值求出A,由周期求出ω,从而得到函数的解析式,再由  ,可得2sin2θ=
,可得2sin2θ= ,再由
,再由  ,可得 cosθ-sinθ<0.求出 (cosθ-sinθ)2 的值,即可求得cosθ-sinθ的值.
,可得 cosθ-sinθ<0.求出 (cosθ-sinθ)2 的值,即可求得cosθ-sinθ的值.
解答:解:由函数f(x)=Asin(ωx)的图象可得A=2,由 ×
× =
= ,解得ω=2.
,解得ω=2.
∵f(θ)= ,∴2sin2θ=
,∴2sin2θ= . 再由
. 再由 ,可得 cosθ-sinθ<0.
,可得 cosθ-sinθ<0.
由于 (cosθ-sinθ)2=1-2sinθcosθ=1-sin2θ=1- =
= ,
,
∴cosθ-sinθ=- .
.
故选A.
点评:本题主要考查利用y=Asin(ωx+∅)的图象特征,由函数y=Asin(ωx+∅)的部分图象求解析式,属于中档题.
 ,可得2sin2θ=
,可得2sin2θ= ,再由
,再由  ,可得 cosθ-sinθ<0.求出 (cosθ-sinθ)2 的值,即可求得cosθ-sinθ的值.
,可得 cosθ-sinθ<0.求出 (cosθ-sinθ)2 的值,即可求得cosθ-sinθ的值.解答:解:由函数f(x)=Asin(ωx)的图象可得A=2,由
 ×
× =
= ,解得ω=2.
,解得ω=2.∵f(θ)=
 ,∴2sin2θ=
,∴2sin2θ= . 再由
. 再由 ,可得 cosθ-sinθ<0.
,可得 cosθ-sinθ<0.由于 (cosθ-sinθ)2=1-2sinθcosθ=1-sin2θ=1-
 =
= ,
,∴cosθ-sinθ=-
 .
.故选A.
点评:本题主要考查利用y=Asin(ωx+∅)的图象特征,由函数y=Asin(ωx+∅)的部分图象求解析式,属于中档题.

练习册系列答案
相关题目
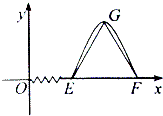 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2008)的值等于
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2008)的值等于 函数f(x)=Asin(ωx+?)(其中A>0,ω>0,
函数f(x)=Asin(ωx+?)(其中A>0,ω>0,