题目内容
17.在中俄两国联合军事反恐演习中,为了准确分析形势,军方在底面上选择相距$\sqrt{3}$km的C,D两点,以测出对方两目标A和B的距离,经测量的:∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,试求出A,B之间的距离.分析 利用△ACD的边角关系得出AC,在△BCD中,由正弦定理即可得出BC,在△ACB中利用余弦定理即可得出AB.
解答 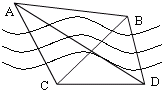 解:在△ACD中,∠ADC=30°,∠ACD=120°,∴∠CAD=30°.
解:在△ACD中,∠ADC=30°,∠ACD=120°,∴∠CAD=30°.
∴AC=CD=$\sqrt{3}$.
在△BDC中,∠CBD=180°-(45°+75°)=60°.
由正弦定理,得BC=$\frac{\sqrt{3}sin75°}{sin60°}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
由余弦定理,得AB2=AC2+BC2-2AC•BC•cos∠BCA
=($\sqrt{3}$)2+($\frac{\sqrt{6}+\sqrt{2}}{2}$)2-2$\sqrt{3}$×$\frac{\sqrt{6}+\sqrt{2}}{2}$×cos75°=5.
∴AB=$\sqrt{5}$.
∴两目标A、B之间的距离为$\sqrt{5}$km.
点评 本题主要考查正弦定理和余弦定理在解三角形中的综合运用.熟练掌握正弦定理和余弦定理是解题的关键.

练习册系列答案
相关题目
8. 《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属醉酒驾车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.
《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属醉酒驾车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.
某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,下面图表是对这20人血液中酒精含量进行检查所得结果的数据表和频率分布直方图.
(1)根据频率表和直方图分别求出x,y,m,n,并补充完整频率分布直方图;
(注:只需补全[40,50)与[70,80)两段,其他段的已经画好)
(2)从血液酒精浓度在[70,90)范围内的驾驶员中任取3人,求至多有1人属于醉酒驾车的概率.
 《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属醉酒驾车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.
《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属醉酒驾车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,下面图表是对这20人血液中酒精含量进行检查所得结果的数据表和频率分布直方图.
| 酒精含量(单位:mg/100ml) | [20,30) | [30,40) | [40,50) | [50,60) |
| 人数 | 3 | 4 | x | 1 |
| 酒精含量(单位:mg/100ml) | [60,70) | [70,80) | [80,90) | [90,100] |
| 人数 | y | 3 | m | n |
(注:只需补全[40,50)与[70,80)两段,其他段的已经画好)
(2)从血液酒精浓度在[70,90)范围内的驾驶员中任取3人,求至多有1人属于醉酒驾车的概率.
5.函数f(x)=x3-3x2+7的极值是( )
| A. | 有极大值无极小值 | B. | 有极小值无极大值 | ||
| C. | 无极大值也无极小值 | D. | 既有极大值也无极小值 |
12.在等比数列{an}(n∈N*)中,若a1=1,a4=$\frac{1}{8}$,则该数列的前12项和为( )
| A. | 2-$\frac{1}{{2}^{4}}$ | B. | 2-$\frac{1}{{2}^{2}}$ | C. | 2-$\frac{1}{{2}^{10}}$ | D. | 2-$\frac{1}{{2}^{11}}$ |
6.“x>0”是“$\frac{1}{x}$>2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.已知a>0,如果P=$\sqrt{a}$+$\sqrt{a+3}$,Q=$\sqrt{a+1}$+$\sqrt{a+2}$,则( )
| A. | P>Q | B. | P<Q | ||
| C. | P=Q | D. | P与Q无法比较大小 |
 如图,正三棱柱ABC-A1B1C1中,D是BC的中点AA1=AB=1
如图,正三棱柱ABC-A1B1C1中,D是BC的中点AA1=AB=1