Question

（2012•资阳三模）已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜

π

2

）部分图象如图所示．
（1）求f（x）的解析式；
（2）若f（

α

2

-

π

6

）=

8 3

7

，cos（α-β）=

13

14

（0＜β＜α＜

α

2

），求β．

Answer 1

分析：（1）根据函数的最大值，得A=2，再由周期公式得ω=2．最后根据当x=

π

12

时f（x）取最大值2，列式并解之得φ=

π

3

，从而得出f（x）的解析式；
（2）由f（

α

2

-

π

6

）=

8 3

7

结合函数表达式，得sinα的值，根据同角三角函数的关系得出cosα的值．再根据0＜β＜α＜

α

2

和cos（α-β）=

13

14

算出sin（α-β）=

3 3

14

，最后利用配角：β=α-（α-β）算出cosβ的值，从而得出β的值．

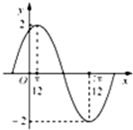
解答：解：（1）由图可得函数的最大值为2，故A=2，
又∵

T

2

=

7π

12

-

π

12

=

π

2

，
∴T=π，得ω=

2π

T

=2，
此时f（x）=2sin（2x+φ），（4分）
∵当x=

π

12

时，f（x）取最大值2，
∴2sin(2×

π

12

+φ)=2，得

π

6

+φ=

π

2

+2kπ，k∈Z
因为|φ|＜

π

2

，所以取k=0，得φ=

π

3

．
∴f（x）的解析式为f(x)=2sin(2x+

π

3

)．（6分）
（2）由（I）得f(

α

2

-

π

6

)=2sinα=

8 3

7

，∴sinα=

4 3

7

，
∵0＜α＜

π

2

，∴cosα=

1-sin2α

=

1-( 4 3 7 )2

=

1

7

，（8分）
由0＜β＜α＜

π

2

，得0＜α-β＜

π

2

，
又∵cos(α-β)=

13

14

，
∴sin(α-β)=

1-cos2(α-β)

=

1-( 13 14 )2

=

3 3

14

．（10分）
因此，cosβ=cos[α-（α-β）]=cosαcos（α-β）+sinαsin（α-β）
=

1

7

×

13

14

+

4 3

7

×

3 3

14

=

1

2

，
∴结合β为锐角，得β=

π

3

．（12分）

点评：本题根据三角函数部分图象确定函数的表达式，并根据表达式求角．着重考查了三角函数的恒等变换及化简求值，由y=Asin（ωx+φ）的部分图象确定其解析式等知识，属于中档题．