题目内容
已知等比数列{an}中，a1+a3=10，a4+a6=
.(1)求数列{an}的通项公式；
(2)求证：
解：(1)设等比数列{an}的公比为q,则根据条件，得
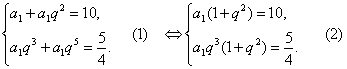
由（2）÷（1）得q3=,q=
.
把q=
代入（1）得a1=8.
从而an=a1qn-1=8·(
)n-1=(
)n-4.
即数列{an}的通项公式为an=(
)n-4.
(2)证明:
=
=
=
=(
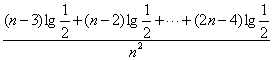
)lg
=-
.
因此所求的结论成立.
练习册系列答案
相关题目
.