题目内容
(12分)圆、椭圆、双曲线都有对称中心,统称为有心圆锥曲线,它们统一的标准方程为![]() .圆的很多优美性质可以类比推广到有心圆锥曲线中,如圆的“垂径定理”的逆定理:圆的平分弦(不是直径)的直径垂直于弦. 类比推广到有心圆锥曲线:已知直线
.圆的很多优美性质可以类比推广到有心圆锥曲线中,如圆的“垂径定理”的逆定理:圆的平分弦(不是直径)的直径垂直于弦. 类比推广到有心圆锥曲线:已知直线![]() 与曲线
与曲线![]() :
:![]() 交于
交于![]() 两点,
两点,![]() 的中点为
的中点为![]() ,若直线
,若直线![]() 和
和![]() (
(![]() 为坐标原点)的斜率都存在,则
为坐标原点)的斜率都存在,则![]() .这个性质称为有心圆锥曲线的“垂径定理”.
.这个性质称为有心圆锥曲线的“垂径定理”.
(Ⅰ)证明有心圆锥曲线的“垂径定理”;
(Ⅱ)利用有心圆锥曲线的“垂径定理”解答下列问题:
① 过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
② 过点![]()
![]() 作直线
作直线![]() 与有心圆锥曲线
与有心圆锥曲线![]() 交于
交于![]() 两点,是否存在这样的直线
两点,是否存在这样的直线![]() 使点
使点![]() 为线段
为线段![]() 的中点?若存在,求直线
的中点?若存在,求直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
解析:(Ⅰ)证明 设![]()

相减得 ![]()
注意到 ![]()
有 ![]()
![]()
即 ![]() …………………………………………5分
…………………………………………5分
(Ⅱ)①设![]()
![]() 由垂径定理,
由垂径定理,![]()
即 ![]()
化简得 ![]()
当![]() 与
与![]() 轴平行时,
轴平行时,![]() 的坐标也满足方程.
的坐标也满足方程.
故所求![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() ;
;
…………………………………………8分
② 假设过点P(1,1)![]() 作直线
作直线![]() 与有心圆锥曲线
与有心圆锥曲线![]() 交于
交于![]() 两点,且P为
两点,且P为![]() 的中点,则
的中点,则
![]()
由于![]()
![]()
直线![]() ,即
,即![]() ,代入曲线
,代入曲线![]() 的方程得
的方程得
![]()
即 ![]()
由 ![]() 得
得![]() .
.
故当![]() 时,存在这样的直线,其直线方程为
时,存在这样的直线,其直线方程为![]() ;
;

练习册系列答案
相关题目
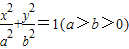 中的推广(不必证明):
中的推广(不必证明):