题目内容
在△ABC中,点M为边AB的中点,若
∥
,且
=x
+y
(x≠0),则
=
| OP |
| OM |
| OP |
| OA |
| OB |
| y |
| x |
1
1
.分析:由点M为边AB的中点,得出
=
(
+
),再由
∥
且
=x
+y
,建立关于x、y的等式,化简可得x=y,从而得到
=1.
| OM |
| 1 |
| 2 |
| OA |
| OB |
| OP |
| OM |
| OP |
| OA |
| OB |
| y |
| x |
解答:解:∵点M为边AB的中点,
∴
=
,即
-
=
-
由此可得
=
(
+
)
∵
∥
,且
=x
+y
(x≠0),
∴存在实数λ,使
=λ
,即
(
+
)=λ(x
+y
)
由此可得λx=λy=
,得到x=y,所以
=1
故答案为:1
∴
| AM |
| MB |
| OM |
| OA |
| OB |
| OM |
由此可得
| OM |
| 1 |
| 2 |
| OA |
| OB |
∵
| OP |
| OM |
| OP |
| OA |
| OB |
∴存在实数λ,使
| OM |
| OP |
| 1 |
| 2 |
| OA |
| OB |
| OA |
| OB |
由此可得λx=λy=
| 1 |
| 2 |
| y |
| x |
故答案为:1
点评:本题以三角形的中线为例,求平行向量之间的线性关系,着重考查了三角形中线的性质和平面向量的基本定理及其意义等知识,属于中档题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
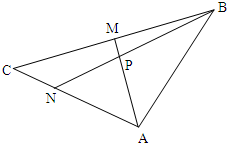 如图,在△ABC中,点M为BC的中点,A、B、C三点坐标分别为(2,-2)、(5,2)、(-3,0),点N在AC上,且
如图,在△ABC中,点M为BC的中点,A、B、C三点坐标分别为(2,-2)、(5,2)、(-3,0),点N在AC上,且 ∥
∥ ,且
,且 ,则
,则 = .
= . ∥
∥ ,且
,且 ,则
,则 = .
= . ,AM与BN的交点为P,求:
,AM与BN的交点为P,求: 所成的比λ的值;
所成的比λ的值;