题目内容
甲、乙两人进行射击训练,命中率分别为| 2 |
| 3 |
| 1 |
| 4 |
(1)求乙射击的命中率;
(2)若甲射击2次,乙射击1次,两人共命中的次数记为ε,求ε的分布列和数学期望.
分析:对于(1)求乙射击的命中率,因为已知乙射击2次均未命中的概率为
,又未命中的概率为1减去命中的概率,列出等式即可.
对于(2)两人共命中的次数记为ε,求ε的分布列和数学期望.因为两人共射击了3次,故ξ可能的取值为0,1,2,3,根据相互独立事件的乘法公式分别求得每种可能性的概率,即可得到分布列,再根据期望公式求得期望即可.
| 1 |
| 4 |
对于(2)两人共命中的次数记为ε,求ε的分布列和数学期望.因为两人共射击了3次,故ξ可能的取值为0,1,2,3,根据相互独立事件的乘法公式分别求得每种可能性的概率,即可得到分布列,再根据期望公式求得期望即可.
解答:解:(1)设“甲射击一次命中”为事件A,“乙射击一次命中”为事件B
由题意得(1-P(B))2=(1-P)2=
解得P=
或P=
(舍去),
故乙射击的命中率为
.
(2)由题意和(1)知P(A)=
,P(
)=
,P(B)=
,P(
)=
.
ξ可能的取值为0,1,2,3,
故P(ξ=0)=P(
)P(
)P(
)=
×
×
=
P(ξ=1)=2P(A)P(
)P(
)+P(
)P(
)P(B)=2×
×
×
+
×
×
=
.P(ξ=2)=1-P(ξ=0)-P(ξ=1)-P(ξ=3)=1-
-
-
=
P(ξ=3)=P(A)P(A)P(B)=
×
×
=
故ξ的分布列为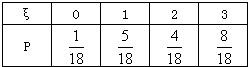
由此得ξ的数学期望Eξ=0×
+1×
+2×
+3×
=
.
由题意得(1-P(B))2=(1-P)2=
| 1 |
| 4 |
解得P=
| 1 |
| 2 |
| 3 |
| 2 |
故乙射击的命中率为
| 1 |
| 2 |
(2)由题意和(1)知P(A)=
| 2 |
| 3 |
. |
| A |
| 1 |
| 3 |
| 1 |
| 2 |
. |
| B |
| 1 |
| 2 |
ξ可能的取值为0,1,2,3,
故P(ξ=0)=P(
. |
| A |
. |
| A |
. |
| B |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 18 |
. |
| A |
. |
| B |
. |
| A |
. |
| A |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 18 |
| 1 |
| 18 |
| 5 |
| 18 |
| 4 |
| 18 |
| 8 |
| 18 |
P(ξ=3)=P(A)P(A)P(B)=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 4 |
| 18 |
故ξ的分布列为

由此得ξ的数学期望Eξ=0×
| 1 |
| 18 |
| 5 |
| 18 |
| 4 |
| 18 |
| 8 |
| 18 |
| 37 |
| 18 |
点评:此题主要考查离散型随机变量的分布列和期望的求法,其中应用到相互独立事件的概率乘法公式,题目覆盖知识点较多,但都属于基本的考点,属于中档题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目