题目内容
已知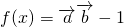 ,其中向量
,其中向量 ,(x∈R).
,(x∈R).
(1) 求f(x)的最小正周期和最小值;
(2) 在△ABC中,角A、B、C的对边分别为a、b、c,若 ,a=2
,a=2 ,b=8,求边长c的值.
,b=8,求边长c的值.
解:∵(1)f(x)= -1=(sin2x,2cosx)•(
-1=(sin2x,2cosx)•( ,cosx)-1
,cosx)-1
= sin2x+2cos2x-1=
sin2x+2cos2x-1= sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+ )
)
∴f(x)的最小正周期为π,最小值为-2
(2)f(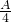 )=2sin(
)=2sin( +
+ )=
)=
∴sin( +
+ )=
)=
∴ +
+ =
= ∴A=
∴A= 或A=π(舍去)
或A=π(舍去)
由余弦定理得a2=b2+c2-2bccosA
52=64+c2-8c即c2-8c+12=0
从而c=2或c=6
分析:先利用向量的数量积的坐标表示及辅助角公式对函数整理可得,f(x)=2sin(2x+ )
)
(1)利用周期公式T= 可求ω,观察函数可知最小值-2
可求ω,观察函数可知最小值-2
(2)由 代入整理可得,sin(
代入整理可得,sin( +
+ )=
)= ,从而可求A,然后利用余弦定理a2=b2+c2-2bccosA可求c的值.
,从而可求A,然后利用余弦定理a2=b2+c2-2bccosA可求c的值.
点评:本题以向量的数量积的坐标表示为切入点,考查了辅助角 asinx+bcosx= 把函数化为一个角的三角函数,进而可以借助于该函数研究函数的相关性质,还考查了由三角函数值求角及由余弦定理求解三角形等知识的综合运用.
把函数化为一个角的三角函数,进而可以借助于该函数研究函数的相关性质,还考查了由三角函数值求角及由余弦定理求解三角形等知识的综合运用.
 -1=(sin2x,2cosx)•(
-1=(sin2x,2cosx)•( ,cosx)-1
,cosx)-1=
 sin2x+2cos2x-1=
sin2x+2cos2x-1= sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+ )
)∴f(x)的最小正周期为π,最小值为-2
(2)f(
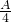 )=2sin(
)=2sin( +
+ )=
)=
∴sin(
 +
+ )=
)=
∴
 +
+ =
= ∴A=
∴A= 或A=π(舍去)
或A=π(舍去)由余弦定理得a2=b2+c2-2bccosA
52=64+c2-8c即c2-8c+12=0
从而c=2或c=6
分析:先利用向量的数量积的坐标表示及辅助角公式对函数整理可得,f(x)=2sin(2x+
 )
)(1)利用周期公式T=
 可求ω,观察函数可知最小值-2
可求ω,观察函数可知最小值-2(2)由
 代入整理可得,sin(
代入整理可得,sin( +
+ )=
)= ,从而可求A,然后利用余弦定理a2=b2+c2-2bccosA可求c的值.
,从而可求A,然后利用余弦定理a2=b2+c2-2bccosA可求c的值.点评:本题以向量的数量积的坐标表示为切入点,考查了辅助角 asinx+bcosx=
 把函数化为一个角的三角函数,进而可以借助于该函数研究函数的相关性质,还考查了由三角函数值求角及由余弦定理求解三角形等知识的综合运用.
把函数化为一个角的三角函数,进而可以借助于该函数研究函数的相关性质,还考查了由三角函数值求角及由余弦定理求解三角形等知识的综合运用. 
练习册系列答案
相关题目
 ,其中向量
,其中向量 ,(x∈R).
,(x∈R). ,a=2
,a=2 ,b=8,求边长c的值.
,b=8,求边长c的值. ,其中向量
,其中向量 ,(x∈R).
,(x∈R). ,a=2
,a=2 ,b=8,求边长c的值.
,b=8,求边长c的值. ,其中向量
,其中向量 ,(x∈R).
,(x∈R). ,a=2
,a=2 ,b=8,求边长c的值.
,b=8,求边长c的值. ,其中向量
,其中向量 ,(x∈R).
,(x∈R). ,a=2
,a=2 ,b=8,求边长c的值.
,b=8,求边长c的值.