题目内容
在正方体ABCD—A1B1C1D1中,O为AC与BD的交点,G为CC1的中点.求证:A1O⊥平面GBD.
分析:要证线面垂直,只要证线线垂直,要证线线垂直,只要证向量的数量积为零,只要用基底表示向量,再求数量积.
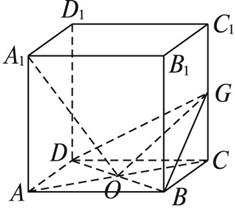
证明:设
则a·b=0,b·c=0,a·c=0.
而
∴
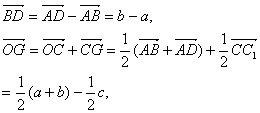
=(c+
a+
b)·(b-a)
=c·(b-a)+
(a+b)·(b-a)
=c·b-c·a+
(b2-a2)
=
(｜b｜2-｜a｜2)=0,
=(c+
a+
b)(
a+
b-
c)
=
(a+b)2+
c·(a+b)-
c2
=
(a2+b2)-
c2
=
(｜a｜2+｜b｜2)-
｜c｜2=0.
∴A1O⊥BD,A1O⊥OG.
又∵BD∩OG=O,
∴A1O⊥平面GBD.
练习册系列答案
寒假学与练系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）