题目内容
幂指函数
在求导时，可运用对数法：在函数解析式两边求对数得
，两边同时求导得
，于是
，运用此方法可以探求得知
的一个单调递增区间为
（ ）
A． 
B．
C．
D．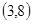
【答案】
A
【解析】解：设f（x）=x，g（x）=
，所以f′（x）=1，g′（x）=-
所以，y′=
×（-lnx+ ）=
×∵x＞0，∴ ＞0，x2＞0令y′＞0，可得只要 1-lnx＞0∴x∈（0，e）∴y= 的一个单调增区间为（0，e）或它的一个子集即可，故选A
练习册系列答案
相关题目
在求导时，可运用对数法：在函数解析式两边求对数得
，两边同时求导得
，于是
．运用此方法可以探求
的一个单调递增区间是（ ）
B．
C．
D．
在求导时，可运用对数法：在函数解析式两边求对数得
，两边同时求导得
，于是
。运用此方法可以探求得知
的一个单调递增区间为（ ）
在求导时，可运用对数法：在函数解析式两边求对数得
，两边同时求导得
=
，于是
，运用此方法可以探求得知
的一个单调递增区间为
） D．（3，8）
在求导时，可运用对数法：在函数解析式两边求对数得
，两边同时求导得
，于是
，运用此方法可以探求得知
的一个单调递增区间为（ ）