题目内容
已知变量x,y满足约束条件
,则z=3|x|+y的取值范围为
|
[1,11]
[1,11]
.分析:作出可行域,去绝对值可得目标函数z=3|x|+y为“∧”型折线,将它进行平移,可得取最大值和最小值的情形,求解可得范围.
解答:解:由题意作出不等式组
表示的平面区域 (阴影),
(阴影),
其中A(-1,2),B(1,0),C(3,2)
去掉绝对值可得z=3|x|+y=
,
其图象是以(0,z)为顶点,开口向下的“∧”型折线,如图
将折线进行平移,可知当它经过点C(3,2)时,z达到最大值11;
当它经过F(0,1)时,z达到最小值1
∴z=3|x|+y的取值范围为[1,11]
故答案为:[1,11]
|
 (阴影),
(阴影),其中A(-1,2),B(1,0),C(3,2)
去掉绝对值可得z=3|x|+y=
|
其图象是以(0,z)为顶点,开口向下的“∧”型折线,如图
将折线进行平移,可知当它经过点C(3,2)时,z达到最大值11;
当它经过F(0,1)时,z达到最小值1
∴z=3|x|+y的取值范围为[1,11]
故答案为:[1,11]
点评:本题考查二元一次不等式组表示的平面区域和简单的线性规划等知识,属中档题.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
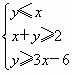 ,则目标函数Z=2x+y的最大值为________.
,则目标函数Z=2x+y的最大值为________. 则目标函数
则目标函数