题目内容
已知两个点M(-3,0)和N(3,0),若直线上存在点P,使|PM|+|PN|=10,则称该直线为“A型直线”,则下列直线
①x=6②y=-5③y=x④y=2x+1中为“A型直线”的是
①x=6②y=-5③y=x④y=2x+1中为“A型直线”的是
③④
③④
(填上所有正确结论的序号)分析:求出P的轨迹方程,画出图象,即可判断①x=6②y=-5③y=x④y=2x+1中为“A型直线”的条数.
解答:解:已知两个点M(-3,0)和N(3,0),使|PM|+|PN|=10,
所以P的轨迹方程为:
+
=1.
画出椭圆与①x=6②y=-5③y=x④y=2x+1的图象.
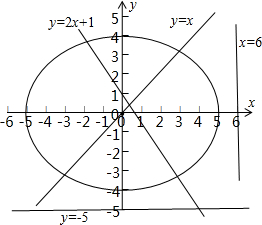
由图象可知,①x=6②y=-5与椭圆没有交点,不存在直线上存在点P,使|PM|+|PN|=10,
③y=x④y=2x+1与椭圆有交点,所以直线上存在点P,使|PM|+|PN|=10.
“A型直线”是③④.
故答案为:③④.
所以P的轨迹方程为:
| x2 |
| 25 |
| y2 |
| 16 |
画出椭圆与①x=6②y=-5③y=x④y=2x+1的图象.
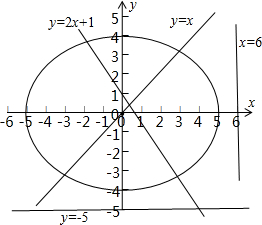
由图象可知,①x=6②y=-5与椭圆没有交点,不存在直线上存在点P,使|PM|+|PN|=10,
③y=x④y=2x+1与椭圆有交点,所以直线上存在点P,使|PM|+|PN|=10.
“A型直线”是③④.
故答案为:③④.
点评:本题考查新定义,椭圆的定义,椭圆与直线的位置关系,考查计算能力,作图能力.

练习册系列答案
相关题目