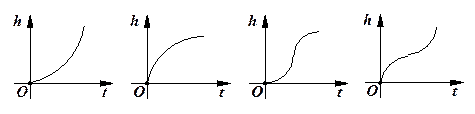题目内容
设二次函数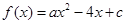 (
(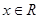 )的值域为
)的值域为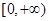 ,则
,则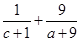 的最大值为
的最大值为
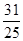
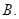
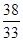
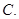
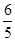
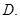
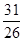
C
解析考点:基本不等式;二次函数的性质.
分析:由于二次函数f(x)=ax2-4x+c的值域为[0,+∞),所以a>0,且△=0,从而得到a,c的关系等式,再利用a,c的关系等式解出a,把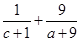 转化为只含一个变量的代数式利用均值不等式进而求解.
转化为只含一个变量的代数式利用均值不等式进而求解.
解:因为二次函数f(x)=ax2-4x+c的值域为[0,+∞),
所以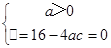 ?ac=4?c=
?ac=4?c=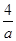 ,
,
所以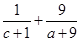 =
= +
+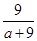 =
= =1+
=1+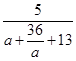
由于a+ ≥12(当且仅当a=6时取等号)
≥12(当且仅当a=6时取等号)
所以1+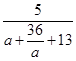 ≤1+
≤1+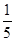 =
=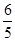 .
.
故答案为:C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 的图像如图所示,则
的图像如图所示,则 的解析式可能是
的解析式可能是
A. | B. |
C. | D. |
如果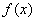 是定义在
是定义在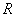 的增函数,且
的增函数,且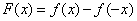 ,那么
,那么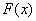 一定是
一定是
A.奇函数,且在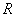 上是增函数 上是增函数 | B.奇函数,且在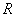 上是减函数 上是减函数 |
C.偶函数,且在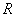 上是增函数 上是增函数 | D.偶函数,且在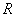 上是减函数 上是减函数 |
下列函数 中,满足“对任意
中,满足“对任意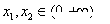 ,当
,当 时,都有
时,都有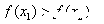 ”的是( )
”的是( )
A. = =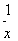 | B. = =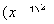 | C. = =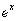 | D.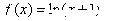 |
已知函数f(x)= 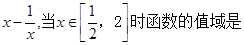 ( )
( )
A.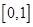 | B.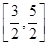 | C.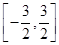 | D.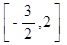 |
若函数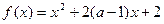 在区间(-∞,4]上是减函数,则实数a的取值范围是 ( )
在区间(-∞,4]上是减函数,则实数a的取值范围是 ( )
| A.a≥3 | B.a≤-3 | C.a<5 | D.a≥-3 |
已知函数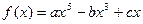 ,且
,且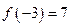 ,则
,则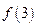 的值为( )
的值为( )
| A.13 | B.-13 | C.7 | D.-7 |
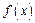 是定义在
是定义在 上的函数,且对于任意的
上的函数,且对于任意的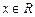 ,有
,有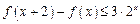 ,
,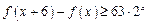 ,若
,若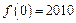 ,则
,则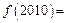 ( )
( )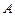 .
.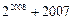
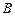 .
.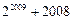
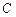 .
.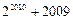
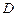 .
.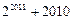
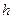 随时间
随时间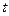 变化的可能图象是( )
变化的可能图象是( )