题目内容
15.已知B,C两点在圆O:x2+y2=1上,A(a,0)为x轴上一点,且a>l.给出以下命题:①$\overrightarrow{OA}$•$\overrightarrow{OC}$的最小值为一1;
②△OBC面积的最大值为1;
③若a=$\sqrt{2}$,且直线AB,AC都与圆O相切,则△ABC为正三角形;
④若a=$\sqrt{2}$,且$\overrightarrow{AB}$=λ$\overrightarrow{BC}$(λ>0),则当△OBC面积最大时,|AB|=$\frac{\sqrt{6}-\sqrt{2}}{2}$;
⑤若a=$\frac{\sqrt{5}}{2}$,且$\overrightarrow{AB}$=$λ\overrightarrow{BC}$,圆O上的点D满足$\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OD}$,则直线BC的斜率是$±\frac{1}{2}$.
其中正确的是⑤(写出所有正确命题的编号).
分析 ①设C(cosθ,sinθ)(θ∈(cosθ,sinθ),θ∈[0,2π).可得$\overrightarrow{OA}$•$\overrightarrow{OC}$=acosθ(a>1),可得最小值,即可判断出正误;
②不妨取B(1,0),则△OBC面积=$\frac{1}{2}×1×sinθ$$≤\frac{1}{2}$,即可判断出正误;
③若a=$\sqrt{2}$,且直线AB,AC都与圆O相切,则∠BAO=∠CAO=45°,即可判断出△ABC的形状,即可判断出正误;
④若a=$\sqrt{2}$,且$\overrightarrow{AB}$=λ$\overrightarrow{BC}$(λ>0),可知:A,B,C三点共线,设AB:my=x-$\sqrt{2}$(m<0),联立与圆的方程联立化为$(1+{m}^{2}){y}^{2}+2\sqrt{2}my$+1=0,△>0,利用根与系数的关系可得|BC|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$,原点O直线AC的距离d=$\frac{\sqrt{2}}{\sqrt{1+{m}^{2}}}$,可得S△OBC=$\frac{1}{2}|BC|d$,再利用基本不等式的性质即可得出,即可判断出正误;
⑤若a=$\frac{\sqrt{5}}{2}$,且$\overrightarrow{AB}$=$λ\overrightarrow{BC}$,设B(x1,y1),C(x2,y2),D(x0,y0),直线AB的方程为:y=$k(x-\frac{\sqrt{5}}{2})$,与圆的方程联立化为(4+4k2)x2-$4\sqrt{5}{k}^{2}$x+5k2-4=0,△>0.利用圆O上的点D满足$\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OD}$,可得x0=x1+x2,y0=y1+y2,代入圆的方程化简即可解出,即可判断出正误.
解答 解:①设C(cosθ,sinθ)(θ∈(cosθ,sinθ),θ∈[0,2π).∴$\overrightarrow{OA}$•$\overrightarrow{OC}$=acosθ(a>1),因此最小值为-a,故不正确;
②不妨取B(1,0),则△OBC面积=$\frac{1}{2}×1×sinθ$$≤\frac{1}{2}$,其最大值为$\frac{1}{2}$,因此不正确;
③若a=$\sqrt{2}$,且直线AB,AC都与圆O相切,则∠BAO=∠CAO=45°,则△ABC为等腰直角三角形,因此不正确;
④若a=$\sqrt{2}$,且$\overrightarrow{AB}$=λ$\overrightarrow{BC}$(λ>0),可知:A,B,C三点共线,设AB:my=x-$\sqrt{2}$(m<0),联立$\left\{\begin{array}{l}{my=x-\sqrt{2}}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,化为$(1+{m}^{2}){y}^{2}+2\sqrt{2}my$+1=0,△>0,|m|>1.∴y1+y2=$\frac{-2\sqrt{2}m}{1+{m}^{2}}$,y1y2=$\frac{1}{1+{m}^{2}}$,
∴|BC|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$2\sqrt{\frac{{m}^{2}-1}{{m}^{2}+1}}$,原点O直线AC的距离d=$\frac{\sqrt{2}}{\sqrt{1+{m}^{2}}}$,∴S△OBC=$\frac{1}{2}|BC|d$=$\frac{1}{2}×$$2\sqrt{\frac{{m}^{2}-1}{{m}^{2}+1}}$×$\frac{\sqrt{2}}{\sqrt{1+{m}^{2}}}$=$\sqrt{2}$×$\sqrt{\frac{{m}^{2}-1}{(1+{m}^{2})^{2}}}$=$\sqrt{2}$$\sqrt{\frac{1}{{m}^{2}-1+\frac{4}{{m}^{2}-1}+4}}$≤$\sqrt{2}×\sqrt{\frac{1}{4+4}}$=$\frac{1}{2}$,当且仅当m2=3时取等号,即△OBC面积取得最大值$\frac{1}{2}$,此时|AB|=2×$\sqrt{\frac{3-1}{3+1}}$=1,因此不正确;
⑤若a=$\frac{\sqrt{5}}{2}$,且$\overrightarrow{AB}$=$λ\overrightarrow{BC}$,设B(x1,y1),C(x2,y2),D(x0,y0),直线AB的方程为:y=$k(x-\frac{\sqrt{5}}{2})$,
联立$\left\{\begin{array}{l}{y=k(x-\frac{\sqrt{5}}{2})}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,化为(4+4k2)x2-$4\sqrt{5}{k}^{2}$x+5k2-4=0,△>0,∴x1+x2=$\frac{4\sqrt{5}{k}^{2}}{4+4{k}^{2}}$,y1+y2=k(x1+x2)-$\sqrt{5}$k
=$-\frac{4\sqrt{5}k}{4+4{k}^{2}}$,∵圆O上的点D满足$\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OD}$,∴x0=x1+x2=$\frac{4\sqrt{5}{k}^{2}}{4+4{k}^{2}}$,y0=y1+y2=$-\frac{4\sqrt{5}k}{4+4{k}^{2}}$,∴$(\frac{4\sqrt{5}{k}^{2}}{4+4{k}^{2}})^{2}$+$(-\frac{4\sqrt{5}k}{4+4{k}^{2}})^{2}$=1,化为4k4+3k2-1=0,解得$k=±\frac{1}{2}$,∴直线BC的斜率是$±\frac{1}{2}$,正确.
综上可得:只有⑤正确.
故答案为:⑤.
点评 本题综合考查了直线与圆的相交问题转化为方程联立可得根与系数的关系、弦长公式、点到直线的距离公式、向量数量积运算性质、三角形面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | {3} | B. | {x|x≤2,或x=3} | ||
| C. | {x|x<-2或-2<x≤2,或x=3} | D. | {x|x<-2,或-2<x≤2} |
| 乙队胜的概率 | 乙队平的概率 | 乙队负的概率 | |
| 与丙 队比赛 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 与丁队比赛 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
(Ⅰ)选拔赛结束,求乙队积4分的概率;
(Ⅱ)设随机变量X为选拔赛结束后乙队的积分,求随机变量X的分布列与数学期望;
(Ⅲ)在目前的积分情况下,M同学认为:乙队至少积4分才能确保出线,N同学认为:乙队至少积5分才能确保出线.你认为谁的观点对?或是两者都不对?(直接写结果,不需证明)
| A. | M=N | B. | M∪N=R | C. | N?M | D. | M?N |
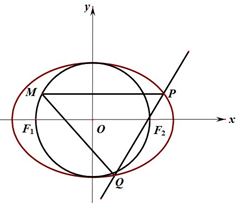 如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.
如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.