Question

已知直线x-y+1=0经过椭圆S：的一个焦点和一个顶点．
（1）求椭圆S的方程；
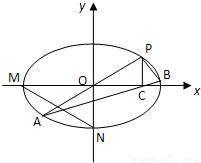
（2）如图，M，N分别是椭圆S的顶点，过坐标原点的直线交椭圆于P、A两点，其中P在第一象限，过P作x轴的垂线，垂足为C，连接AC，并延长交椭圆于点B，设直线PA的斜率为k．
①若直线PA平分线段MN，求k的值；
②对任意k＞0，求证：PA⊥PB．

Answer 1

【答案】分析：（1）在直线x-y+1=0中，令x=0得y=1；令y=0得x=-1，故c=b=1，a²=2，由此能求出椭圆方程．
（2）①，N（0，-1），M、N的中点坐标为（，），所以
②法一：将直线PA方程y=kx代入，解得，记，则P（m，mk），A（-m，-mk），于是C（m，0），故直线AB方程为，代入椭圆方程得（k²+2）x²-2k²mx+k²m²-8=0，由此能够证明PA⊥PB．
法二：设P（x，y），A（-x，-y），B（x₁，y₁），则C（x，0），由A、C、B三点共线，知=，由此能够证明PA⊥PB．
解答：解：（1）在直线x-y+1=0中令x=0得y=1；令y=0得x=-1，
由题意得c=b=1，
∴a²=2，
则椭圆方程为．
（2）①，N（0，-1），
M、N的中点坐标为（，），
所以．
②解法一：将直线PA方程y=kx代入，
解得，
记，
则P（m，mk），A（-m，-mk），于是C（m，0），
故直线AB方程为，
代入椭圆方程得（k²+2）x²-2k²mx+k²m²-8=0，
由，
因此，
∴，，
∴，
∴，故PA⊥PB．
解法二：由题意设P（x，y），A（-x，-y），B（x₁，y₁），则C（x，0），
∵A、C、B三点共线，
∴=，
又因为点P、B在椭圆上，
∴，，
两式相减得：，
∴=-=-1，
∴PA⊥PB．
点评：本题考查直线和椭圆的性质和应用，考查运算求解能力，推理论证能力；考查化归与转化思想．对数学思维的要求比较高，有一定的探索性．综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答．