题目内容
(本小题满分12分)已知数列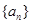 ,
,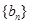 与函数
与函数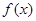 ,
,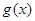 ,
,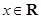 满足条件:
满足条件: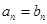 ,
,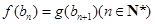 .
.
(I)若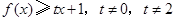 ,
,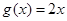 ,
,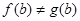 ,
,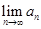 存在,求
存在,求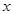 的取值范围;
的取值范围;
(II)若函数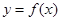 为
为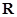 上的增函数,
上的增函数,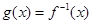 ,
,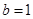 ,
,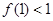 ,证明对任意
,证明对任意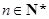 ,
,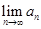 (用
(用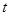 表示).
表示).
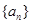 ,
,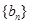 与函数
与函数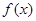 ,
,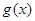 ,
,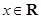 满足条件:
满足条件: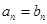 ,
,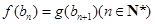 .
.(I)若
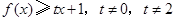 ,
,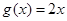 ,
,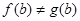 ,
,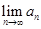 存在,求
存在,求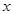 的取值范围;
的取值范围;(II)若函数
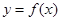 为
为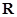 上的增函数,
上的增函数,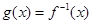 ,
,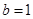 ,
,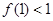 ,证明对任意
,证明对任意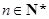 ,
,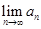 (用
(用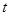 表示).
表示).(I)-2<t<2且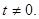
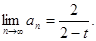
(II)对任意的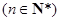 ,
,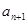 <
<
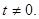
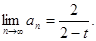
(II)对任意的
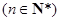 ,
,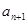 <
<
解法一:由题设知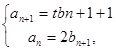 得
得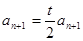 ,又已知
,又已知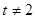 ,可得
,可得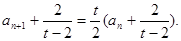
由
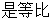 其首项为
其首项为 .于是
.于是
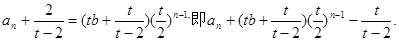
又liman存在,可得0< <1,所以-2<t<2且
<1,所以-2<t<2且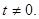
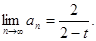
解法二.由题设知tbn+1=2bn+1,且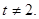 可得
可得

由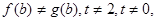 可知
可知 ,所以
,所以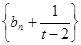 是首项为
是首项为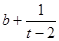 ,公
,公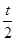 的等比数列.
的等比数列.
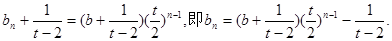
由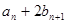 可知,若
可知,若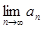 存在,则
存在,则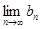 存在.于是可得0<
存在.于是可得0<
 <1,所以-1<t
<1,所以-1<t .
.
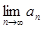 =2
=2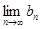
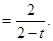
解法三:由题设知tbn+1=2bn+1,即
 ①
①
于是有
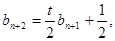 ②
②
②-①得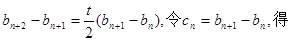
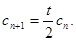
由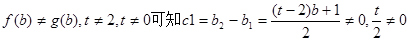 ,所以
,所以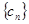 是首项为b公比为
是首项为b公比为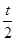 的等比数列,于是
的等比数列,于是
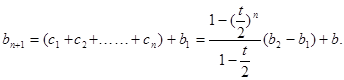
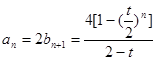 (b2-b1)+2b.
(b2-b1)+2b.
又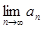 存在,可得0<
存在,可得0<
 <1,所以-2<t<2且
<1,所以-2<t<2且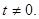
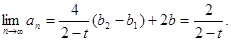
说明:数列 通项公式的求法和结果的表达形式均不唯一,其他过程和结果参照以标准.
通项公式的求法和结果的表达形式均不唯一,其他过程和结果参照以标准.
(Ⅱ)证明:因为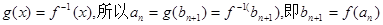 .
.
下面用数学归纳法证明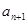 <
<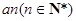 .
.
(1)当n=1时,由f(x)为增函数,且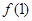 <1,得
<1,得
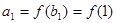 <1
<1
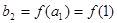 <1
<1
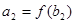 <
< ,
,
即 <
< ,结论成立.
,结论成立.
(2)假设n=k时结论成立,即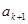 <
<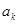 .由f(x)为增函数,得
.由f(x)为增函数,得
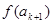 <f
<f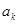 即
即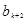 <
<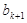 进而得
进而得
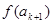 <f(
<f(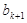 )即
)即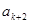 <
<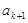 .
.
这就是说当n=k+1时,结论也成立.
根据(1)和(2)可知,对任意的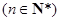 ,
,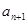 <
< .
.
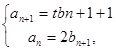 得
得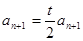 ,又已知
,又已知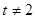 ,可得
,可得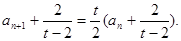
由

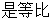 其首项为
其首项为 .于是
.于是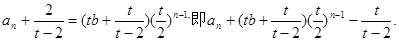
又liman存在,可得0<
 <1,所以-2<t<2且
<1,所以-2<t<2且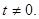
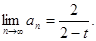
解法二.由题设知tbn+1=2bn+1,且
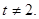 可得
可得
由
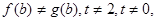 可知
可知 ,所以
,所以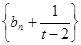 是首项为
是首项为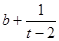 ,公
,公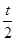 的等比数列.
的等比数列.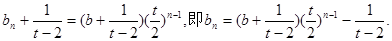
由
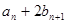 可知,若
可知,若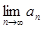 存在,则
存在,则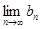 存在.于是可得0<
存在.于是可得0<
 <1,所以-1<t
<1,所以-1<t .
.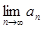 =2
=2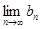
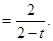
解法三:由题设知tbn+1=2bn+1,即
 ①
①于是有
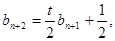 ②
②②-①得
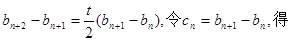
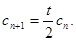
由
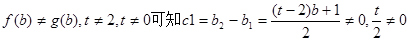 ,所以
,所以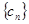 是首项为b公比为
是首项为b公比为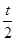 的等比数列,于是
的等比数列,于是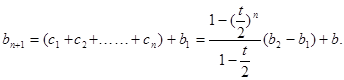
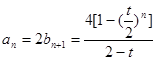 (b2-b1)+2b.
(b2-b1)+2b.又
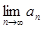 存在,可得0<
存在,可得0<
 <1,所以-2<t<2且
<1,所以-2<t<2且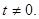
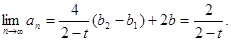
说明:数列
 通项公式的求法和结果的表达形式均不唯一,其他过程和结果参照以标准.
通项公式的求法和结果的表达形式均不唯一,其他过程和结果参照以标准.(Ⅱ)证明:因为
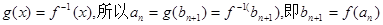 .
.下面用数学归纳法证明
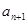 <
<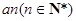 .
.(1)当n=1时,由f(x)为增函数,且
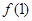 <1,得
<1,得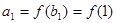 <1
<1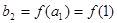 <1
<1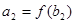 <
< ,
,即
 <
< ,结论成立.
,结论成立.(2)假设n=k时结论成立,即
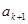 <
<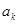 .由f(x)为增函数,得
.由f(x)为增函数,得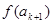 <f
<f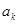 即
即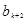 <
<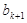 进而得
进而得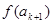 <f(
<f(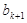 )即
)即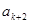 <
<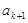 .
.这就是说当n=k+1时,结论也成立.
根据(1)和(2)可知,对任意的
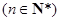 ,
,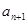 <
< .
.
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
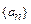 满足:
满足: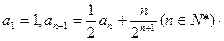
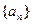 的通项公式;
的通项公式;  (2)证明:
(2)证明: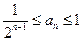 ;
;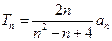 ,且
,且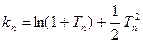 ,证明:
,证明: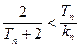 .
.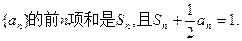
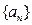 的通项公式;
的通项公式;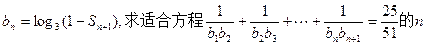 的值。
的值。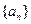 中,
中,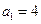 且对任意
且对任意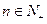 均有:
均有: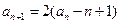
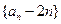 是等比数列;
是等比数列;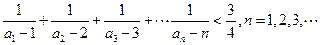
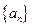 中,
中,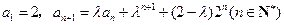 ,其中
,其中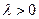 .
.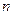 项和
项和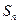 ;
;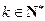 ,使得
,使得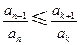 对任意
对任意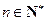 均成立.
均成立.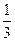 ,记为
,记为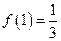 ;②当从A口输入自然数
;②当从A口输入自然数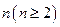 时,在B口得到的结果
时,在B口得到的结果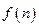 是前一个结果
是前一个结果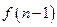 的
的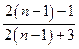 倍.
倍.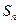 为数列
为数列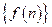 的前
的前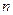 项的和。当从B口得到399的倒数时,求此时对应的
项的和。当从B口得到399的倒数时,求此时对应的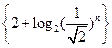 中的第10项是 。
中的第10项是 。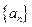 满足
满足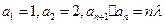 (
(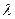 为常数,
为常数,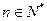 ),则
),则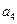 等于( )
等于( )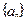 的前
的前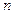 项和
项和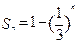 ,把
,把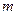 行第
行第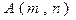
 ,则
,则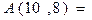 _____________.
_____________.