题目内容
两直线(m+2)x-y+m=0,x+y=0 与x轴相交且能构成三角形,则m满足的条件是 .
【答案】分析:找出直线(m+2)x-y+m=0过的定点,在平面直角坐标系中,通过画图就能分析得到能构成三角形的直线(m+2)x-y+m=0的斜率范围,从而求得m的取值范围.
解答: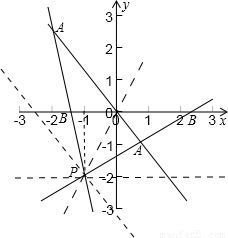 解:由(m+2)x-y+m=0,得:2x-y+m(x+1)=0,联立
解:由(m+2)x-y+m=0,得:2x-y+m(x+1)=0,联立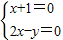 ,得
,得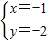 ,
,
所以直线(m+2)x-y+m=0过定点P(-1,-2),且直线(m+2)x-y+m=0与x轴不垂直,
如图所示,
由图形可知,要使过P点的直线与x轴相交、与y=x相交且能构成三角形,
该直线的斜率要大于0,且不等于2,斜率为负值时应小于-1,
所以有m+2<-1或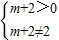 ,解得:m∈(-∞,-3)∪(-2,0)∪(0,+∞).
,解得:m∈(-∞,-3)∪(-2,0)∪(0,+∞).
故答案为m∈(-∞,-3)∪(-2,0)∪(0,+∞).
点评:本题考查了三点共线,两条直线平行与倾斜角、斜率的关系,考查了数形结合的解题思想,训练了线系方程过定点的求法,此题是易错题.
解答:
 解:由(m+2)x-y+m=0,得:2x-y+m(x+1)=0,联立
解:由(m+2)x-y+m=0,得:2x-y+m(x+1)=0,联立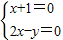 ,得
,得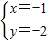 ,
,所以直线(m+2)x-y+m=0过定点P(-1,-2),且直线(m+2)x-y+m=0与x轴不垂直,
如图所示,
由图形可知,要使过P点的直线与x轴相交、与y=x相交且能构成三角形,
该直线的斜率要大于0,且不等于2,斜率为负值时应小于-1,
所以有m+2<-1或
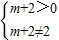 ,解得:m∈(-∞,-3)∪(-2,0)∪(0,+∞).
,解得:m∈(-∞,-3)∪(-2,0)∪(0,+∞).故答案为m∈(-∞,-3)∪(-2,0)∪(0,+∞).
点评:本题考查了三点共线,两条直线平行与倾斜角、斜率的关系,考查了数形结合的解题思想,训练了线系方程过定点的求法,此题是易错题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目