题目内容
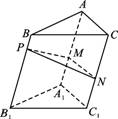
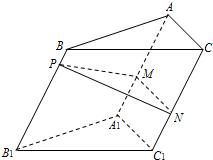
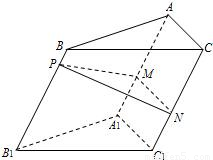
如图,点P为斜三棱柱ABC—A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF·EF·cos∠DFE.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.

解析:(1)证明:∵CC1∥BB1![]() CC1⊥PM,CC1⊥PN,且PM∩PN=P,?
CC1⊥PM,CC1⊥PN,且PM∩PN=P,?
∴CC1⊥平面PMN![]() CC1⊥MN.?
CC1⊥MN.?
(2)在斜三棱柱ABC—A1B1C1中,有SABB1A12=SBCC1B12+SACC1A12-2SBCC1B1·SACC1A1cosα,其中α为平面CC1B1B与平面CC1A1A所组成的二面角.?
∵CC1⊥平面PMN,∴上述的二面角为∠MNP.在△PMN中,PM2=PN2+MN2-2PN·MN·cos
∠MNP![]() PM2CC12=PN2CC12+MN2CC12-2(PN·CC1)·(MN·CC1)cos∠MNP,由于SBCC1B1=PN·CC1,SACC1A1=MN·CC1,SABB1A1=PM·BB1,?
PM2CC12=PN2CC12+MN2CC12-2(PN·CC1)·(MN·CC1)cos∠MNP,由于SBCC1B1=PN·CC1,SACC1A1=MN·CC1,SABB1A1=PM·BB1,?
∴有SABB1A12=SBCC1B12+SACC1A12-2SBCC1B1·SACC1A1cosα.

练习册系列答案
相关题目
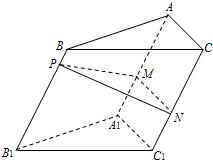 如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.