题目内容
(选修4-4:坐标系与参数方程)直线l的极坐标方程为C:ρcos(θ-
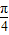 )=3
)=3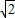 ,圆C:
,圆C: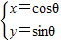 (θ为参数)上的点到直线l的距离值为d,则d的最大值为 .
(θ为参数)上的点到直线l的距离值为d,则d的最大值为 .
【答案】分析:将圆C:参数方程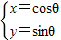 (θ为参数)和直线的极坐标方程ρcos(θ-
(θ为参数)和直线的极坐标方程ρcos(θ-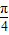 )=3
)=3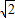 转化为直角坐标方程,再结合直角坐标系下的点到直线的距离公式求解即得.
转化为直角坐标方程,再结合直角坐标系下的点到直线的距离公式求解即得.
解答:解:∵圆C: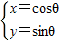 (θ为参数),
(θ为参数),
∴x2+y2=1,
∵直线l的极坐标方程为C:ρcos(θ-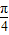 )=3
)=3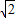 ,
,
∴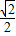 ρcosθ+
ρcosθ+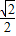 ρsinθ=3
ρsinθ=3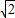 ,
,
∵x=ρcosθ,y=ρsinθ,
∴x+y=6,
∴求圆C上的点到直线l的距离的最大值d,转化为圆心到直线的距离加上圆的半径,
∴圆心到直线的距离为: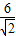 =3
=3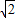 ,
,
∴d=3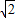 +1;
+1;
故答案为:3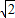 +1;
+1;
点评:本题考查点的极坐标和直角坐标的互化,以及点到直线的距离公式,同时考查了运算求解的能力,属于基础题.
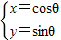 (θ为参数)和直线的极坐标方程ρcos(θ-
(θ为参数)和直线的极坐标方程ρcos(θ-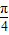 )=3
)=3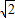 转化为直角坐标方程,再结合直角坐标系下的点到直线的距离公式求解即得.
转化为直角坐标方程,再结合直角坐标系下的点到直线的距离公式求解即得.解答:解:∵圆C:
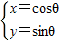 (θ为参数),
(θ为参数),∴x2+y2=1,
∵直线l的极坐标方程为C:ρcos(θ-
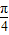 )=3
)=3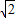 ,
,∴
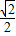 ρcosθ+
ρcosθ+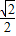 ρsinθ=3
ρsinθ=3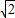 ,
,∵x=ρcosθ,y=ρsinθ,
∴x+y=6,
∴求圆C上的点到直线l的距离的最大值d,转化为圆心到直线的距离加上圆的半径,
∴圆心到直线的距离为:
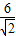 =3
=3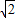 ,
,∴d=3
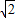 +1;
+1;故答案为:3
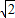 +1;
+1;点评:本题考查点的极坐标和直角坐标的互化,以及点到直线的距离公式,同时考查了运算求解的能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲