题目内容
如图,在三棱锥S—ABC中,△ABC是边长为8的正三角形,SA=SC=2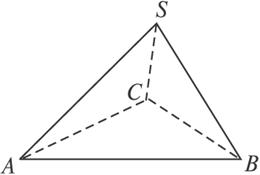
(1)求证:AC⊥SB;
(2)求二面角S-BC-A的正切值.
(1)证明:取AC的中点D,连结SD、BD,
∵SA=SC,D为AC的中点,
∴SD⊥AC.
∵AB=BC,D为AC的中点,
∴BD⊥AC.又SD∩BD=D,
∴AC⊥面SBD.又SB![]() 面SBD,∴AC⊥SB.
面SBD,∴AC⊥SB.
(2)解:过O作OH⊥BC于H,连SH,则SH⊥BC,
∴∠SHO为二面角SBCA的平面角.
∵正△ABC的边长为8,∴BD=4![]() .
.
∵OD=![]() =
=![]() ,
,
∴OB=3![]() .在Rt△OHB中,OH=OB·sin30°=
.在Rt△OHB中,OH=OB·sin30°=![]() OB=
OB=![]()
![]() .
.
在Rt△SOH中,tan∠SHO=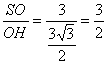
![]() ,
,
即二面角S-BC-A的正切值为![]()
![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC. 如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( )
如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( ) 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2 (2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( )
(2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( ) (2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )
(2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )