题目内容
一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度v(t)=7-3t+ (t的单位:s,v的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是 ( ).
(t的单位:s,v的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是 ( ).
| A.1+25ln 5 | B.8+25ln  |
| C.4+25ln 5 | D.4+50ln 2 |
C
解析

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
如图所示是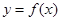 的导数
的导数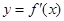 的图像,下列四个结论:
的图像,下列四个结论:
①  在区间
在区间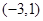 上是增函数;
上是增函数;
② 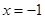 是
是 的极小值点;
的极小值点;
③  在区间
在区间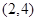 上是减函数,在区间
上是减函数,在区间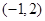 上是增函数;
上是增函数;
④ 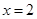 是
是 的极小值点.其中正确的结论是
的极小值点.其中正确的结论是
| A.①②③ |
| B.②③ |
| C.③④ |
| D.①③④ |
已知函数f(x)=ax2+3x-2在点(2,f(2))处的切线斜率为7,则实数a的值为( )
| A.-1 | B.1 | C.±1 | D.-2 |
已知函数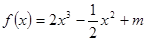 (m为常数)图象上A处的切线与
(m为常数)图象上A处的切线与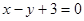 平行,则点A的横坐标是( )
平行,则点A的横坐标是( )
A. | B.1 | C.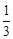 或 或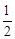 | D. 或 或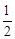 |
函数y=f′(x)是函数y=f(x)的导函数,且函数y=f(x)在点P(x0,f(x0))处的切线为l:y=g(x)=f′(x0)·(x-x0)+f(x0),F(x)="f(x)-g(x)," 如果函数y=f(x)在区间[a,b]上的图象如图所示,且a<x0<b,那么( )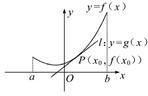
| A.F'(x0)=0,x=x0是F(x)的极大值点 |
| B.F'(x0)=0,x=x0是F(x)的极小值点 |
| C.F'(x0)≠0,x=x0不是F(x)的极值点 |
| D.F'(x0)≠0,x=x0是F(x)的极值点 |
已知函数f(x)=x3+ax2+x+2(a>0)的极大值点和极小值点都在区间(-1,1)内,则实数a的取值范围是( ).
| A.(0,2] | B.(0,2) | C.[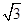 ,2) ,2) | D.(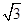 ,2) ,2) |
已知函数f(x)=x(ln x-ax)有两个极值点,则实数a的取值范围是( ).
| A.(-∞,0) | B.(0,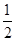 ) ) | C.(0,1) | D.(0,+∞) |
设函数f(x)=x3-4x+a(0<a<2)有三个零点x1,x2,x3,且x1<x2<x3,则下列结论正确的是( ).
| A.x1>-1 | B.x2<0 |
| C.x3>2 | D.0<x2<1 |