Question

已知向量．

（I）若，求COS（﹣x）的值；

（II）记，在△ABC中，角A，B，C的对边分别是a，b，c，且满足（2a﹣c）cosB=bcosC，求函数f（A）的取值范围．

Answer 1

考点：

数量积的坐标表达式；两角和与差的余弦函数；正弦定理．

专题：

计算题．

分析：

（1）利用向量的数量积公式列出方程求出，利用二倍角的余弦公式求出要求的式子的值．

（2）利用三角形中的正弦定理将等式中的边转化为角的正弦值，利用三角形的内角和为180°化简等式，求出角B，求出角A的范围，求出三角函数值的范围．

解答：

解：（1）

∵

∴

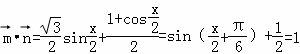
∵（6分）（2）∵（2a﹣c）cosB=bcosC

∴2sinAcosB=sinCcosB+sinBcosC=sin（B+C）=sinA

∵sinA＞0

∴cosB=

∵B∈（0，π），

∴

∴

∵

∴

∵

∴

∴（12分）

点评：

本题考查向量的数量积公式、考查三角形的正弦定理、考查三角形的内角和为180°、考查利用三角函数的单调性求三角函数值的范围．