Question

设{a_n}是等差数列，{b_n}是各项都为正数的等比数列，且a₁=b₁=1，a₂+b₃=a₃+b₂=7．
（1）求{a_n}，{b_n}的通项公式；
（2）记c_n=a_n-2010，n∈N*，A_n为数列{c_n}的前n项和，当n为多少时A_n取得最大值或最小值？
（3）（理）是否存在正数K，使得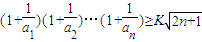对一切n∈N*均成立，若存在，求出K的最大值，若不存在，说明理由．
（4）（文）求数列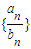的前n项和S_n．

Answer 1

【答案】分析：（1）先设公差是d，公比是q，根据a₁=b₁=1，a₂+b₃=a₃+b₂=7，列出关于d、q的方程组，解出d、q即可求出求a_n，b_n的通项公式；
（2）当c_n≥0，求出n≥1005.5，当c_n＞0，n≥1006，进而可知当n=1005时，A_n取得最小值；
（3）因为等价于K≤F（n）_min，其中，研究其单调得出F（n）是递增的，从而
（4）由于．利用错位相减法求得Sn=；
解答：解：（1）设a_n的公差为d，b_n的公比为q，则依题意有q＞0且
解得d=2，q=2．（2分）
所以a_n=1+（n-1）d=2n-1，b_n=q^n-1=2^n-1．（2分）
（2）因为c_n=a_n-2010=2n-2011≥0?n≥1005.5，所以，当1≤n≤1005时，c_n＜0，当n≥1006时，c_n＞0．（2分）
所以当n=1005时，A_n取得最小值．（2分）
（3）等价于K≤F（n）_min，
其中；（2分）
因为：?4n²+8n+4＞4n²+8n+3?4＞3显然成立，所以F（n）是递增的．（4分）
从而．（2分）
或因为：，
所以：F（n）是递增的．（4分）；
从而．（2分）
（4）．①（2分）
②
②-①得（2分）
==（3分）
=．（1分）
点评：本题主要考查了数列通项公式和前n项和的求法以及数列的最值问题，对于等差数列和等比数列相乘形式数列，一般采取错位相减的办法求数列的前n项和，一定要熟练掌握．