Question

在Rt△ABC中，∠C=90°，且角A、B、C所对的边a、b、c满足a+b=cx，则实数x的取值范围是________．

Answer 1

分析：利用三角形的边的关系，以及勾股定理基本不等式，即可推出x的范围．
解答：因为在Rt△ABC中，∠C=90°，且角A、B、C所对的边a、b、c，
所以有a+b＞c，即a+b=cx＞c，∴x＞1，因为a²+b²=c²，
所以a+b=cx化为（a+b）²=（a²+b²）x²，
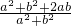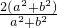x²=≤=2；
x，
综上x∈．
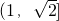故答案为：．
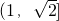点评：本题是中档题，考查三角形的基本性质，勾股定理基本不等式的应用，考查计算能力．