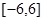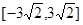题目内容
在边长为 的正三角形ABC中,设
的正三角形ABC中,设 ,则
,则 等于( )
等于( )
| A.0 | B.1 | C.3 | D.-3 |
D
解析试题分析:∵三角形ABC为边长为 的正三角形,∴
的正三角形,∴ ,故选D
,故选D
考点:本题考查了数量积的运用
点评:熟练掌握向量的夹角及数量积的定义是解决此类问题的关键,属基础题

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案在ΔABC中,已知D是AB边上一点,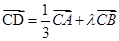 ,则实数λ=
,则实数λ=
A.-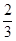 | B.-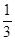 | C.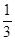 | D.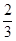 |
已知 ,则
,则
A. | B. | C. | D. |
若向量 满足
满足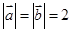 ,且
,且 ,则向量
,则向量 的夹角为
的夹角为
| A.30° | B.45° | C.60° | D.120° |
已知向量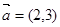 ,
,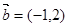 ,若
,若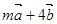 与
与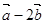 共线,则 ( )
共线,则 ( )
A. | B. | C.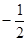 | D.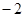 |
已知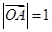 ,
,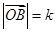 ,
,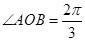 ,点C在
,点C在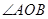 内,
内, 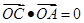 ,若
,若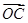 =2m
=2m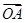 +m
+m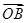 (
(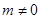 ),则
),则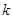 =( )
=( )
| A.1 | B.2 | C.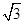 | D.4 |
已知向量 ,若
,若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
在平行四边形ABCD中,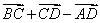 等于( )
等于( )
A. | B.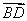 | C.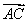 | D. |
 :
: ,四边形
,四边形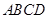 为圆
为圆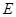 、
、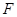 分别为边
分别为边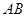 、
、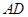 的中点,当正方形
的中点,当正方形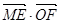 的取值范围是( )
的取值范围是( )