题目内容
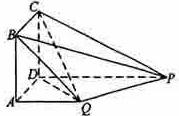
如图，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA=AB=
PD．
（I）证明：PQ⊥平面DCQ；
（II）求棱锥Q—ABCD的的体积与棱锥P—DCQ的体积的比值．
解：（I）由条件知PDAQ为直角梯形
因为QA⊥平面ABCD，所以平面PDAQ⊥平面ABCD，交线为AD.
又四边形ABCD为正方形，DC⊥AD，所以DC⊥平面PDAQ，可得PQ⊥DC.
在直角梯形PDAQ中可得DQ=PQ=
PD，则PQ⊥QD
所以PQ⊥平面DCQ. ………………6分
（II）设AB=a.
由题设知AQ为棱锥Q—ABCD的高，所以棱锥Q—ABCD的体积
由（I）知PQ为棱锥P—DCQ的高，而PQ=
，△DCQ的面积为
，
所以棱锥P—DCQ的体积为
故棱锥Q—ABCD的体积与棱锥P—DCQ的体积的比值为1.…………12分
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
如图，四边形ABCD与A′ABB′都是边长为a的正方形，点E是A′A的中点，A′A⊥平面ABCD．
如图，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA=AB=
如图，四边形ABCD为矩形，且AD=2，AB=1，PA⊥平面ABCD，PA=1，E为BC的中点．
如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD
如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=