题目内容

试判别，抛物线中以焦点弦为直径的圆与准线的位置关系.

解：设准线为l，点A、B到准线l的距离为d₁、d₂，AB中点到l的距离为d，

由题意知：d=(d₁+d₂)=(|FA|+|FB|)=|AB|，

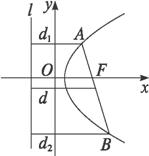
所以以AB为直径的圆与准线相切.

练习册系列答案

金牌夺冠一卷OK系列答案

核心360小学生赢在100系列答案

期末闯关100分系列答案

家校导学系列答案

新每课一练系列答案

开心蛙状元作业系列答案

黄冈海淀大考卷单元期末冲刺100分系列答案

课时掌控随堂练习系列答案

课堂新动态系列答案

一课一练一本通系列答案

相关题目

已知抛物线y²=2px（p＞0），点P（m，n）为抛物线上任意一点，其中m≥0．
（1）判断抛物线与正比例函数的交点个数；
（2）定义：凡是与圆锥曲线有关的圆都称为该圆锥曲线的伴随圆，如抛物线的内切圆就是最常见的一种伴随圆．此外还有以焦点弦为直径的圆，以及以焦点弦为弦且过顶点的圆等．同类的伴随圆构成一个圆系，圆系中有无数多个圆．求证：抛物线内切圆系方程为：（x-p-m）²+y²=p²+2pm（其中m为参数且m≥0）；
（3）请研究抛物线以焦点弦为直径的伴随圆，推导出其圆系方程，并写出一个关于它的正确命题．

经过抛物线的所有焦点弦中，弦长的最小值为（）

A、p B、2p C、4p D、不确定

已知抛物线y²=2px（p＞0），点P（m，n）为抛物线上任意一点，其中m≥0．
（1）判断抛物线与正比例函数的交点个数；
（2）定义：凡是与圆锥曲线有关的圆都称为该圆锥曲线的伴随圆，如抛物线的内切圆就是最常见的一种伴随圆．此外还有以焦点弦为直径的圆，以及以焦点弦为弦且过顶点的圆等．同类的伴随圆构成一个圆系，圆系中有无数多个圆．求证：抛物线内切圆系方程为：（x-p-m）²+y²=p²+2pm（其中m为参数且m≥0）；
（3）请研究抛物线以焦点弦为直径的伴随圆，推导出其圆系方程，并写出一个关于它的正确命题．

已知抛物线y²=2px（p＞0），点P（m，n）为抛物线上任意一点，其中m≥0．
（1）判断抛物线与正比例函数的交点个数；
（2）定义：凡是与圆锥曲线有关的圆都称为该圆锥曲线的伴随圆，如抛物线的内切圆就是最常见的一种伴随圆．此外还有以焦点弦为直径的圆，以及以焦点弦为弦且过顶点的圆等．同类的伴随圆构成一个圆系，圆系中有无数多个圆．求证：抛物线内切圆系方程为：（x-p-m）²+y²=p²+2pm（其中m为参数且m≥0）；
（3）请研究抛物线以焦点弦为直径的伴随圆，推导出其圆系方程，并写出一个关于它的正确命题．