题目内容
已知椭圆![]() +
+![]() =1(a>b>0)的右焦点为F,经过点F作倾斜角为135°的直线l交椭圆于A、B两点,线段AB的中点为M,且直线AB与OM的夹角为
=1(a>b>0)的右焦点为F,经过点F作倾斜角为135°的直线l交椭圆于A、B两点,线段AB的中点为M,且直线AB与OM的夹角为![]() ,且tan
,且tan![]() =3,求这个椭圆的离心率.
=3,求这个椭圆的离心率.
答案:
解析:
提示:
解析:
|
解:设点A(x1,y1)、B(x2,y2),AB的中点为M(x0,y0),则 两式相减可得kAB= 所以a2y0=b2x0. 又kOM= 故kOM= 所以1-e2= 解析:本题先根据题意求出直线AB的斜率,再依据直线与椭圆的方程联立消去其中一个未知数,找到相应的两个交点A、B的横(或纵)坐标之间的关系,从而表示出相应的中点M的坐标,从而将问题解决. |
提示:
|
对于有关直线与椭圆的交点问题的解决,通常联立直线与椭圆的方程消去其中的一个未知数,从而利用根与系数间的关系将两个交点的横(或纵)坐标间的关系找到,再利用已知条件解决相关的问题. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
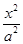 +
+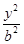 =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点。若AB的中点坐标为(1,-1),则E的方程为 (
)
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点。若AB的中点坐标为(1,-1),则E的方程为 (
)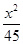 +
+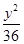 =1
B、
=1
B、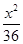 +
+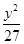 =1
=1 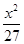 +
+ =1
D、
=1
D、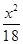 +
+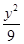 =1
=1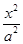 +
+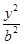 =1(a>b>0)的一个焦点是圆x2+y2-6x+8=0的圆心,且短轴长为8,则椭圆的左顶点为( )
=1(a>b>0)的一个焦点是圆x2+y2-6x+8=0的圆心,且短轴长为8,则椭圆的左顶点为( ) 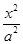 +
+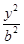 =1(a>b>0)的左右顶点为
=1(a>b>0)的左右顶点为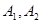 ,上下顶点为
,上下顶点为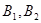 ,
左右焦点为
,
左右焦点为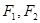 ,若
,若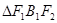 为等腰直角三角形(1)求椭圆的离心率(2)若
为等腰直角三角形(1)求椭圆的离心率(2)若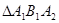 的面积为6
的面积为6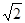 ,求椭圆的方程
,求椭圆的方程 +
+ =1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P.若
=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P.若 =2
=2 ,则椭圆的离心率是( )
,则椭圆的离心率是( ) B.
B. C.
C. D.
D.